(本小題滿分14分)
某商場以100元/件的價格購進一批襯衣，以高于進貨價的價格出售，銷售期有淡季與旺季之分，通過市場調查發現：
①銷售量
(件)與襯衣標價
(元/件)在銷售旺季近似地符合函數關系：
，在銷售淡季近似地符合函數關系：
，其中
為常數；
②在銷售旺季，商場以140元/件的價格銷售能獲得最大銷售利潤；
③若稱①中
時的標價為襯衣的“臨界價格”，則銷售旺季的“臨界價格”是銷售淡季的“臨界價格”的1.5倍．
請根據上述信息，完成下面問題：
(Ⅰ)填出表格中空格的內容：
|
銷售關系 |
標價(元/件) |
銷售量 |
銷售總利潤 (元/件)的函數關系式 |
|
旺季 |
|
|
|
|
淡季 |
|
|
|
(Ⅱ)在銷售淡季，該商場要獲得最大銷售利潤，襯衣的標價應定為多少元/件？
（1）
|
|
標價（元/件） |
銷售量 |
銷售總利潤 |
|
旺季 |
|
|
|
|
淡季 |
|
|
|
（2）故在銷售淡季，商場要獲得最大銷售利潤，襯衣的標價應定為110元/件
【解析】
解：（Ⅰ）
|
|
標價（元/件） |
銷售量 |
銷售總利潤 |
|
旺季 |
|
|
|
|
淡季 |
|
|
|
6分
（Ⅱ）在（Ⅰ）的表達式
中，由
可知，
在銷售旺季，當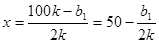
時，利潤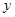
取得最大值；
在銷售淡季，當
時，利潤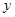取得最大值.7分
下面分銷售旺季和淡季進行討論：
由②知，在銷售旺季，商場以140元/件的價格出售時，能獲得最大利潤.
因此在銷售旺季，當標價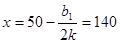
時，利潤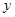取得最大值。此時，
，銷售量為
. 10分
令
得
，故在銷售旺季，襯衣的“臨界價格”為180元/件.
∴由③知，在銷售淡季，襯衣的“臨界價格”為120元/件.可見在銷售淡季，當標價
時，
，∴
，∴
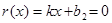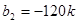. 12分
∴在銷售淡季，當
時，利潤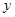取得最大值，
故在銷售淡季，商場要獲得最大銷售利潤，襯衣的標價應定為110元/件. 12分
科目：高中數學 來源： 題型：
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目：高中數學 來源： 題型：
（本小題滿分14分）設橢圓C1的方程為
(a＞b＞0)，曲線C2的方程為y=
，且曲線C1與C2在第一象限內只有一個公共點P。（1）試用a表示點P的坐標；（2）設A、B是橢圓C1的兩個焦點，當a變化時，求△ABP的面積函數S(a)的值域；（3）記min{y1,y2,……,yn}為y1,y2,……,yn中最小的一個。設g(a)是以橢圓C1的半焦距為邊長的正方形的面積，試求函數f(a)=min{g(a), S(a)}的表達式。
查看答案和解析>>
科目：高中數學 來源：2011年江西省撫州市教研室高二上學期期末數學理卷（A） 題型：解答題
（本小題滿分14分）
已知
=2，點（
）在函數
的圖像上，其中
=
.
(1)證明：數列
}是等比數列；
（2）設
，求
及數列{
}的通項公式；
（3）記
，求數列{
}的前n項和
，并證明
.
查看答案和解析>>
科目：高中數學 來源：2015屆山東省威海市高一上學期期末考試數學試卷（解析版） 題型：解答題
(本小題滿分14分)
某網店對一應季商品過去20天的銷售價格及銷售量進行了監測統計發現，第
天(
)的銷售價格(單位：元)為
，第天的銷售量為
，已知該商品成本為每件25元.
（Ⅰ）寫出銷售額
關于第天的函數關系式；
（Ⅱ）求該商品第7天的利潤；
（Ⅲ）該商品第幾天的利潤最大？并求出最大利潤.
查看答案和解析>>
科目：高中數學 來源：2011-2012學年廣東省高三下學期第一次月考文科數學試卷（解析版） 題型：解答題
（本小題滿分14分）已知
的圖像在點
處的切線與直線
平行.
⑴ 求
，
滿足的關系式；
⑵ 若
上恒成立，求的取值范圍；
⑶ 證明：
（
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
數量關系
、
或
)
(元)與標價
（件）（含
、
或
）
（元/件）的函數關系式
