已知向量
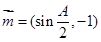
,
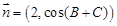
,

為銳角
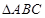
的內(nèi)角,
其對應邊為
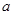
,
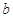
,

.
(Ⅰ)當
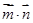
取得最大值時,求角

的大小;
(Ⅱ)在(Ⅰ)成立的條件下,當
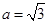
時,求
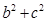
的取值范圍.
解:(Ⅰ)
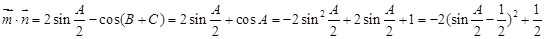
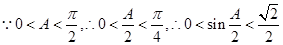
,
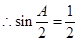
時,即
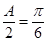
時,
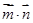
取得最大值,
∴
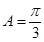
……………………………………………….4分
(Ⅱ)由正弦定理可知
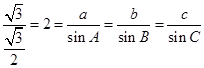
,
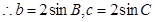
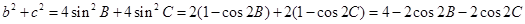
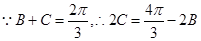
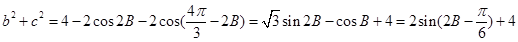
…………………6分
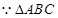
為銳角三角形
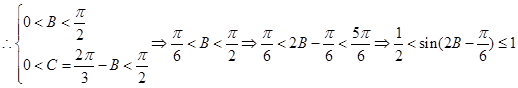
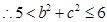
……………………………………………………………….8分
本試題主要是考查了向量的數(shù)量積公式得到三角函數(shù)關系式,以及正弦定理和與余弦定理的綜合運用。
(1)由于
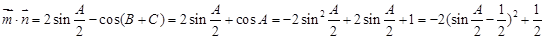
利用三角函數(shù)中角A的范圍得到結論。
(2)根據(jù)由正弦定理可知
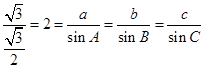
,
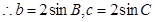
,然后利用余弦定理得到
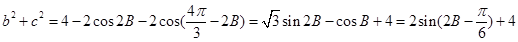
進而得到范圍,
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題12分)已知
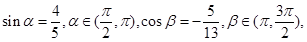
求:
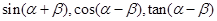
。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分14分)在

中,
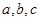
分別是

所對的邊,已知

,

,三角形的面積為

,(1)求C的大小;(2)求

的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
當函數(shù)
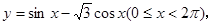
取最大值時,

。
查看答案和解析>>

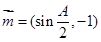 ,
,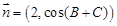 ,
, 為銳角
為銳角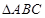 的內(nèi)角,
的內(nèi)角,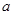 ,
,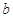 ,
, .
.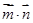 取得最大值時,求角
取得最大值時,求角 的大小;
的大小;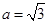 時,求
時,求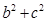 的取值范圍.
的取值范圍.