
在△ABC中,a,b,c分別為∠A,∠B,∠C的對邊.如果a,b,c成等差數(shù)列,∠B=30°,△ABC的面積為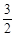 ,那么b=( ).
,那么b=( ).
A.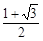 | B.1+ | C.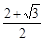 | D.2+ |
B
解析試題分析:根據(jù)等差中項(xiàng)的性質(zhì)可知2b=a+c.平方后整理得a2+c2=4b2-2ac.利用三角形面積求得ac的值,進(jìn)而把a(bǔ)2+c2=4b2-2ac.代入余弦定理求得b的值.:∵a,b,c成等差數(shù)列,∴2b=a+c.平方得a2+c2=4b2-2ac.又△ABC的面積為 ,且∠B=30°,故由S△=
,且∠B=30°,故由S△=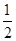 acsinB=
acsinB=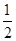 ac•sin30°=
ac•sin30°=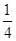 ac=
ac= ,得ac=6,∴a2+c2=4b2-12.由余弦定理
,得ac=6,∴a2+c2=4b2-12.由余弦定理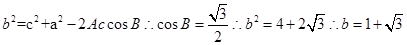 ,故選B
,故選B
考點(diǎn):正弦定理,余弦定理
點(diǎn)評:本題主要考查了解三角形的問題.解題過程中常需要正弦定理,余弦定理,三角形面積公式以及勾股定理等知識.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:單選題
已知等差數(shù)列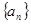 的前三項(xiàng)依次為
的前三項(xiàng)依次為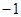 ,
, ,
,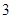 ,則此數(shù)列的通項(xiàng)公式為( )
,則此數(shù)列的通項(xiàng)公式為( )
A.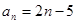 | B.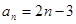 | C.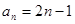 | D.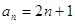 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
在各項(xiàng)均不為零的等差數(shù)列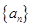 中,若a
中,若a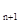 - a
- a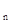
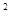 + a
+ a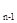 =0(n≥2),則S
=0(n≥2),則S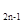 -4n=( )
-4n=( )
A -2 B 0 C 1 D 2
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
一個(gè)樣本容量為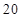 的樣本數(shù)據(jù),它們組成一個(gè)公差不為
的樣本數(shù)據(jù),它們組成一個(gè)公差不為 的等差數(shù)列
的等差數(shù)列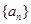 ,若
,若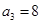 且前
且前 項(xiàng)和
項(xiàng)和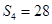 ,則此樣本的平均數(shù)和中位數(shù)分別是
,則此樣本的平均數(shù)和中位數(shù)分別是
A.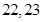 | B.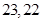 | C.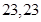 | D.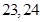 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
若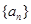 是等差數(shù)列,首項(xiàng)公差
是等差數(shù)列,首項(xiàng)公差 ,
,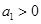 ,且
,且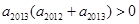 ,則使數(shù)列
,則使數(shù)列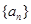 的前n項(xiàng)和
的前n項(xiàng)和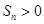 成立的最大自然數(shù)n是 ( )
成立的最大自然數(shù)n是 ( )
| A.4027 | B.4026 | C.4025 | D.4024 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com