
已知橢圓C: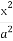 +
+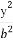 =1(a>b>0).
=1(a>b>0).
(1)若橢圓的長軸長為4,離心率為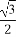 ,求橢圓的標準方程.
,求橢圓的標準方程.
(2)在(1)的條件下,設過定點M(0,2)的直線l與橢圓C交于不同的兩點A,B,且∠AOB為銳角(其中O為坐標原點),求直線l的斜率k的取值范圍.
(3)過原點O任意作兩條互相垂直的直線與橢圓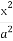 +
+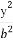 =1(a>b>0)相交于P,S,R,Q四點,設原點O到四邊形PQSR一邊的距離為d,試求d=1時a,b滿足的條件.
=1(a>b>0)相交于P,S,R,Q四點,設原點O到四邊形PQSR一邊的距離為d,試求d=1時a,b滿足的條件.
(1)  +y2=1 (2) k∈(-2,-
+y2=1 (2) k∈(-2,- )∪(
)∪( ,2) (3)
,2) (3) 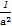 +
+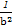 =1
=1
【解析】(1)由已知2a=4,∴a=2,
又e=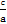 =
= ,∴c=
,∴c=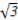 .
.
因此,b2=a2-c2=4-3=1,
∴橢圓的標準方程為 +y2=1.
+y2=1.
(2)顯然直線x=0不滿足題設條件,
可設直線l:y=kx+2,A(x1,y1),B(x2,y2).
由 消去y得(1+4k2)x2+16kx+12=0.
消去y得(1+4k2)x2+16kx+12=0.
∵Δ=(16k)2-4×12(1+4k2)>0,
∴k∈(-∞,- )∪(
)∪( ,+∞) ①
,+∞) ①
又x1+x2=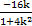 ,x1x2=
,x1x2=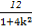 ,
,
由0°<∠AOB<90°⇒ ·
·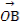 >0,
>0,
∴ ·
·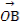 =x1x2+y1y2>0,
=x1x2+y1y2>0,
所以 ·
·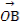 =x1x2+y1y2
=x1x2+y1y2
=x1x2+(kx1+2)(kx2+2)
=(1+k2)x1x2+2k(x1+x2)+4,
∴-2<k<2 ②
由①②得k∈(-2,- )∪(
)∪( ,2).
,2).
(3)由橢圓的對稱性可知PQSR是菱形,原點O到各邊的距離相等.
當P在y軸上,Q在x軸上時,直線PQ的方程為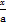 +
+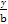 =1,由d=1得
=1,由d=1得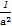 +
+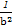 =1,
=1,
當P不在y軸上時,設直線PS的斜率為k,P(x1,kx1),則直線RQ的斜率為-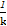 ,Q(x2,-
,Q(x2,-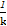 x2),
x2),
由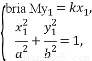 得
得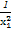 =
=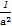 +
+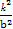 ①
①
同理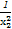 =
=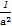 +
+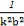 ②
②
在Rt△OPQ中,由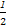 d·|PQ|=
d·|PQ|=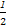 |OP|·|OQ|,
|OP|·|OQ|,
即|PQ|2=|OP|2·|OQ|2.
所以(x1-x2)2+(kx1+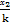 )2
)2
=[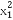 +(kx1)2]·[
+(kx1)2]·[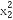 +(
+(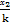 )2],
)2],
化簡得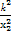 +
+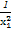 =1+k2,
=1+k2,
k2(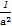 +
+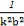 )+
)+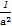 +
+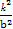 =1+k2,
=1+k2,
即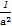 +
+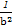 =1.
=1.
綜上,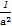 +
+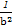 =1.
=1.
【方法技巧】平面向量在平面解析幾何中的應用
平面向量作為數學解題的工具,常與平面解析幾何結合綜合考查,主要涉及向量的數量積、夾角、長度、距離等方面的知識,應用方向主要是平面內點的坐標與對應向量數量積的轉化,通過數量積運算尋找等量關系,使問題轉化,從而使問題獲解.


科目:高中數學 來源:2014年高考數學全程總復習課時提升作業六十九第十章第六節練習卷(解析版) 題型:選擇題
已知P是△ABC所在平面內一點,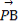 +
+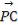 +2
+2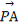 =0,現將一粒黃豆隨機撒在△ABC內,則黃豆落在△PBC內的概率是( )
=0,現將一粒黃豆隨機撒在△ABC內,則黃豆落在△PBC內的概率是( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業八十選修4-5第二節練習卷(解析版) 題型:解答題
已知f(x)=|x+1|+|x-1|,不等式f(x)<4的解集為M.
(1)求M.
(2)當a,b∈M時,證明:2|a+b|<|4+ab|.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十第八章第一節練習卷(解析版) 題型:填空題
經過點(-2,2),且與兩坐標軸所圍成的三角形面積為1的直線l的方程為 .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十第八章第一節練習卷(解析版) 題型:選擇題
已知△ABC三頂點坐標A(1,2),B(3,6),C(5,2),M為AB中點,N為AC中點,則直線MN的方程為( )
(A)2x+y-8=0 (B)2x-y+8=0
(C)2x+y-12=0 (D)2x-y-12=0
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十四第八章第五節練習卷(解析版) 題型:填空題
在平面直角坐標系xOy中,橢圓C的中心為原點,焦點F1,F2在x軸上,離心率為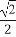 .過F1的直線l交C于A,B兩點,且△ABF2的周長為16,那么C的方程為 .
.過F1的直線l交C于A,B兩點,且△ABF2的周長為16,那么C的方程為 .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十六第八章第七節練習卷(解析版) 題型:解答題
如圖,橢圓C: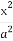 +
+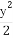 =1的焦點在x軸上,左右頂點分別為A1,A,上頂點為B,拋物線C1,C2分別以A,B為焦點,其頂點均為坐標原點O,C1與C2相交于直線y=
=1的焦點在x軸上,左右頂點分別為A1,A,上頂點為B,拋物線C1,C2分別以A,B為焦點,其頂點均為坐標原點O,C1與C2相交于直線y=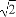 x上一點P.
x上一點P.
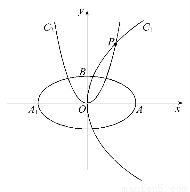
(1)求橢圓C及拋物線C1,C2的方程.
(2)若動直線l與直線OP垂直,且與橢圓C交于不同兩點M,N,已知點Q(-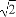 ,0),求
,0),求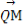 ·
·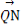 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十八第八章第九節練習卷(解析版) 題型:填空題
設直線l:2x+y-2=0與橢圓x2+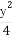 =1的交點為A,B,點P是橢圓上的動點,則使得△PAB的面積為
=1的交點為A,B,點P是橢圓上的動點,則使得△PAB的面積為 的點P的個數為 .
的點P的個數為 .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十九第八章第十節練習卷(解析版) 題型:解答題
給定橢圓C: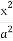 +
+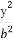 =1(a>b>0),稱圓心在原點O,半徑為
=1(a>b>0),稱圓心在原點O,半徑為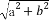 的圓是橢圓C的“準圓”.若橢圓C的一個焦點為F(
的圓是橢圓C的“準圓”.若橢圓C的一個焦點為F(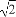 ,0),其短軸上的一個端點到F的距離為
,0),其短軸上的一個端點到F的距離為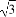 .
.
(1)求橢圓C的方程和其“準圓”的方程.
(2)點P是橢圓C的“準圓”上的一個動點,過動點P作直線l1,l2使得l1,l2與橢圓C都只有一個交點,且l1,l2分別交其“準圓”于點M,N.
①當P為“準圓”與y軸正半軸的交點時,求l1,l2的方程;
②求證:|MN|為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com