
【題目】《山東省高考改革試點方案》規(guī)定:從![]() 年高考開始,高考物理、化學(xué)等六門選考科目的考生原始成績從高到低劃分為
年高考開始,高考物理、化學(xué)等六門選考科目的考生原始成績從高到低劃分為![]() 八個等級.參照正態(tài)分布原則,確定各等級人數(shù)所占比例分別為
八個等級.參照正態(tài)分布原則,確定各等級人數(shù)所占比例分別為![]() .選考科目成績計入考生總成績時,將
.選考科目成績計入考生總成績時,將![]() 至
至![]() 等級內(nèi)的考生原始成績,依照等比例轉(zhuǎn)換法則分別轉(zhuǎn)換到
等級內(nèi)的考生原始成績,依照等比例轉(zhuǎn)換法則分別轉(zhuǎn)換到![]()
![]() 八個分數(shù)區(qū)間,得到考生的等級成績.
八個分數(shù)區(qū)間,得到考生的等級成績.
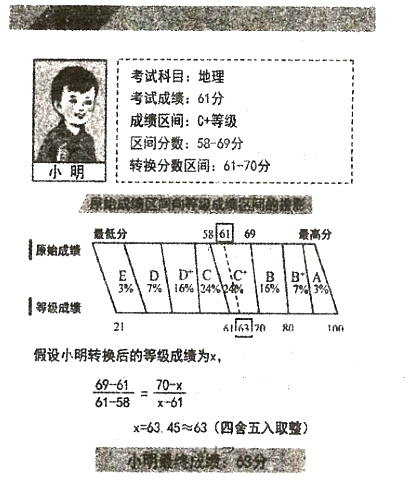
某校![]() 級學(xué)生共
級學(xué)生共![]() 人,以期末考試成績?yōu)樵汲煽冝D(zhuǎn)換了本校的等級成績,為學(xué)生合理選科提供依據(jù),其中物理成績獲得等級
人,以期末考試成績?yōu)樵汲煽冝D(zhuǎn)換了本校的等級成績,為學(xué)生合理選科提供依據(jù),其中物理成績獲得等級![]() 的學(xué)生原始成績統(tǒng)計如下
的學(xué)生原始成績統(tǒng)計如下
成績 | 93 | 91 | 90 | 88 | 87 | 86 | 85 | 84 | 83 | 82 |
人數(shù) | 1 | 1 | 4 | 2 | 4 | 3 | 3 | 3 | 2 | 7 |
(1)從物理成績獲得等級![]() 的學(xué)生中任取
的學(xué)生中任取![]() 名,求恰好有
名,求恰好有![]() 名同學(xué)的等級分數(shù)不小于
名同學(xué)的等級分數(shù)不小于![]() 的概率;
的概率;
(2)待到本級學(xué)生高考結(jié)束后,從全省考生中不放回的隨機抽取學(xué)生,直到抽到![]() 名同學(xué)的物理高考成績等級為
名同學(xué)的物理高考成績等級為![]() 或
或![]() 結(jié)束(最多抽取
結(jié)束(最多抽取![]() 人),設(shè)抽取的學(xué)生個數(shù)為
人),設(shè)抽取的學(xué)生個數(shù)為![]() ,求隨機變量
,求隨機變量![]() 的數(shù)學(xué)期望(注:
的數(shù)學(xué)期望(注: ![]() ).
).
【答案】(1)0.29 (2)見解析
【解析】
(1)設(shè)物理成績獲得等級![]() 的學(xué)生原始成績?yōu)?/span>
的學(xué)生原始成績?yōu)?/span>![]() ,其等級成績?yōu)?/span>
,其等級成績?yōu)?/span>![]() ,由原始成績與等級成績的轉(zhuǎn)換公式得到
,由原始成績與等級成績的轉(zhuǎn)換公式得到![]() 關(guān)于
關(guān)于![]() 的關(guān)系式,即可計算出等級分數(shù)不小于
的關(guān)系式,即可計算出等級分數(shù)不小于![]() 的人數(shù),利用古典概型即可計算出恰好有
的人數(shù),利用古典概型即可計算出恰好有![]() 名同學(xué)的等級分數(shù)不小于
名同學(xué)的等級分數(shù)不小于![]() 的概率。
的概率。
(2)由題意得,隨機抽取![]() 人,等級成績?yōu)?/span>
人,等級成績?yōu)?/span>![]() 或
或![]() 的概率為
的概率為![]() ,然后列出學(xué)生個數(shù)的分布列,即可計算數(shù)學(xué)期望。
,然后列出學(xué)生個數(shù)的分布列,即可計算數(shù)學(xué)期望。
解:(1)設(shè)物理成績獲得等級![]() 的學(xué)生原始成績?yōu)?/span>
的學(xué)生原始成績?yōu)?/span>![]() ,其等級成績?yōu)?/span>
,其等級成績?yōu)?/span>![]() .
.
由轉(zhuǎn)換公式![]() ,得
,得![]() .
.
由![]() ,得
,得![]() .
.
顯然原始成績滿足![]() 的同學(xué)有
的同學(xué)有![]() 人,獲得等級
人,獲得等級![]() 的學(xué)生有
的學(xué)生有![]() 人,
人,
恰好有![]() 名同學(xué)的等級分數(shù)不小于
名同學(xué)的等級分數(shù)不小于![]() 的概率為:
的概率為:![]() .
.
(2)由題意得,隨機抽取![]() 人,其等級成績?yōu)?/span>
人,其等級成績?yōu)?/span>![]() 或
或![]() 的概率為
的概率為![]() .
.
學(xué)生個數(shù)![]() 的可能取值為
的可能取值為![]() ;
;
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ;
;
其數(shù)學(xué)期望是:
![]()
![]()
![]()
其中:
![]() ①
①
![]() ②
②
應(yīng)用錯位相減法“①式-②式”得:
![]()
![]()
![]()
故![]() .
.


 學(xué)期復(fù)習(xí)一本通學(xué)習(xí)總動員期末加暑假延邊人民出版社系列答案
學(xué)期復(fù)習(xí)一本通學(xué)習(xí)總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,設(shè)直線
,設(shè)直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,
兩點,![]() 為線段
為線段![]() 的中點.
的中點.

(1)若直線![]() 的傾斜角為
的傾斜角為![]() ,求
,求![]() 的值;
的值;
(2)設(shè)直線![]() 交直線
交直線![]() 于點
于點![]() ,證明:直線
,證明:直線![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過橢圓的焦點且與長軸垂直的弦長為1.
,過橢圓的焦點且與長軸垂直的弦長為1.
(1)求橢圓C的方程;
(2)設(shè)點M為橢圓上第一象限內(nèi)一動點,A,B分別為橢圓的左頂點和下頂點,直線MB與x軸交于點C,直線MA與y軸交于點D,求證:四邊形ABCD的面積為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個暗箱中有形狀和大小完全相同的3只白球與2只黑球,每次從中取出一只球,取到白球得2分,取到黑球得3分.甲從暗箱中有放回地依次取出3只球.
(1)求甲三次都取得白球的概率;
(2)求甲總得分ξ的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (其中
(其中![]() 為參數(shù)).在以坐標(biāo)原點
為參數(shù)).在以坐標(biāo)原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸建立的極坐標(biāo)系中,曲線
軸正半軸為極軸建立的極坐標(biāo)系中,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,曲線
,曲線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() .
.
(1)求直線![]() 的極坐標(biāo)方程和曲線
的極坐標(biāo)方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若直線![]() 與曲線
與曲線![]() 分別相交于異于原點的點
分別相交于異于原點的點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】兩城市![]() 和
和![]() 相距
相距![]() ,現(xiàn)計劃在兩城市外以
,現(xiàn)計劃在兩城市外以![]() 為直徑的半圓
為直徑的半圓![]() 上選擇一點
上選擇一點![]() 建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關(guān),對城
建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關(guān),對城![]() 和城
和城![]() 的總影響度為城
的總影響度為城![]() 和城
和城![]() 的影響度之和,記
的影響度之和,記![]() 點到城
點到城![]() 的距離為
的距離為![]() ,建在
,建在![]() 處的垃圾處理場對城
處的垃圾處理場對城![]() 和城
和城![]() 的總影響度為
的總影響度為![]() ,統(tǒng)計調(diào)查表明:垃圾處理場對城
,統(tǒng)計調(diào)查表明:垃圾處理場對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數(shù)為4,對城
的距離的平方成反比,比例系數(shù)為4,對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數(shù)為
的距離的平方成反比,比例系數(shù)為![]() ,當(dāng)垃圾處理場建在
,當(dāng)垃圾處理場建在![]() 的中點時,對城
的中點時,對城![]() 和城
和城![]() 的總影響度為0.065;
的總影響度為0.065;
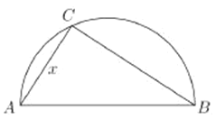
(1)將![]() 表示成
表示成![]() 的函數(shù);
的函數(shù);
(2)判斷![]() 上是否存在一點,使建在此處的垃圾處理場對城
上是否存在一點,使建在此處的垃圾處理場對城![]() 和城
和城![]() 的總影響度最小?若存在,求出該點到城
的總影響度最小?若存在,求出該點到城![]() 的距離;若不存在,說明理由;
的距離;若不存在,說明理由;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1(側(cè)棱垂直于底面的棱柱)中,CA⊥CB,CA=CB=CC1=2,動點D在線段AB上.
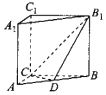
(1)求證:當(dāng)點D為AB的中點時,平面B1CD⊥上平面ABB1A1;
(2)當(dāng)AB=3AD時,求平面B1CD與平面BB1C1C所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列五個命題:
①“![]() ”是“
”是“![]() 為R上的增函數(shù)”的充分不必要條件;
為R上的增函數(shù)”的充分不必要條件;
②函數(shù)![]() 有兩個零點;
有兩個零點;
③集合![]() ,
,![]() ,從A,B中各任意取一個數(shù),則這兩數(shù)之和等于4的概率是
,從A,B中各任意取一個數(shù),則這兩數(shù)之和等于4的概率是![]() ;
;
④動圓C既與定圓![]() 相外切,又與y軸相切,則圓心C的軌跡方程是
相外切,又與y軸相切,則圓心C的軌跡方程是![]() ;
;
⑤若對任意的正數(shù)x,不等式![]() 恒成立,則實數(shù)a的取值范圍是
恒成立,則實數(shù)a的取值范圍是![]() .
.
其中正確的命題序號是________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將紅、黑、藍、白5張紙牌(其中白紙牌有2張)隨機分發(fā)給甲、乙、丙、丁4個人,每人至少分得1張,則下列兩個事件為互斥事件的是( )
A. 事件“甲分得1張白牌”與事件“乙分得1張紅牌”
B. 事件“甲分得1張紅牌”與事件“乙分得1張藍牌”
C. 事件“甲分得1張白牌”與事件“乙分得2張白牌”
D. 事件“甲分得2張白牌”與事件“乙分得1張黑牌”
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com