
已知函數f(x)的定義域為{x| x ≠ kπ,k ∈ Z},且對于定義域內的任何x、y,有f(x - y) = ![]() 成立,且f(a) = 1(a為正常數),當0 < x < 2a時,f(x) > 0.
成立,且f(a) = 1(a為正常數),當0 < x < 2a時,f(x) > 0.
(1) 判斷f(x)奇偶性;
(2) 證明f(x)為周期函數;
(3) 求f (x)在[2a,3a] 上的最小值和最大值.
證明:(1) ∵定義域{x| x ≠ kπ,k∈Z }關于原點對稱,
又f(- x) = f [(a - x) - a]= ![]() =
= ![]()
= 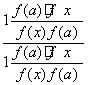 =
= 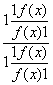 =
= ![]() = - f (x),
= - f (x),
對于定義域內的每個x值都成立.
∴ f (x)為奇函數
(2) 易證:f(x + 4a) = f(x),周期為4a.
(3) f (2a) = f (a + a) = f [a - (- a)]= ![]() =
= ![]() = 0,
= 0,
f (3a) = f (2a + a) = f [2a - (- a)]= ![]() =
= ![]() = - 1.
= - 1.
先證明f (x)在[2a,3a]上單調遞減為此,必須證明x∈(2a,3a) 時,f (x) < 0,
設2a < x < 3a,則0 < x - 2a < a,
∴ f (x - 2a) = ![]() = -
= - ![]() > 0,
> 0,
∴ f (x) < 0
設2a < x1 < x2 < 3a,
則0 < x2 - x1 < a,∴ f (x1) < 0 f (x2) < 0 f (x2 - x1) > 0,
∴ f (x1) - f (x2)= ![]() > 0,∴ f (x1) > f (x2),
> 0,∴ f (x1) > f (x2),
∴ f (x)在[2a,3a]上單調遞減
∴ f (x)在[2a,3a]上的最大值為f (2a) = 0,最小值為f (3a) = - 1.


科目:高中數學 來源: 題型:
| 1 |
| 3 |
| a-3 |
| 2 |
| x | 2 1 |
| x | 2 2 |
| x | 3 1 |
| x | 3 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x |
| 1+x |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| x |
| ||
1+
|
| x |
| 1+x |
| 1 |
| 1+x |
| x |
| 1+x |
| 1+x |
| 1+x |
| 1 | ||
2x+
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 1-x |
| 1 |
| 2 |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| lim |
| n→∞ |
| 4Sn-9Sn |
| 4Sn+1+9Sn+1 |
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| x+1-a |
| a-x |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 1-x |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| sinα | ||
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com