
已知函數(shù)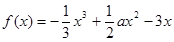 ,
,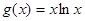
(Ⅰ)當(dāng)a=4時(shí),求函數(shù)f(x)的單調(diào)區(qū)間;
(Ⅱ)求函數(shù)g(x)在區(qū)間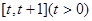 上的最小值;
上的最小值;
(Ⅲ)若存在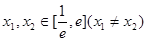 ,使方程
,使方程
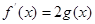 成立,求實(shí)數(shù)a的取值范圍(其中e=2.71828是自然對數(shù)的底數(shù))
成立,求實(shí)數(shù)a的取值范圍(其中e=2.71828是自然對數(shù)的底數(shù))
(Ⅰ)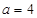 時(shí),
時(shí),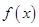 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為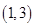 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為 .
.
(Ⅱ)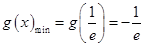 ;(III)實(shí)數(shù)
;(III)實(shí)數(shù) 的取值范圍為
的取值范圍為 .
.
解析試題分析:(Ⅰ)求導(dǎo)數(shù),根據(jù)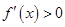 ,
,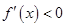 得到函數(shù)的單調(diào)區(qū)間.
得到函數(shù)的單調(diào)區(qū)間.
(Ⅱ)遵循“求導(dǎo)數(shù),求駐點(diǎn),討論單調(diào)性,確定最值”.
(III) 由 可得
可得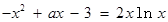
“分離參數(shù)”得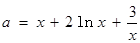 .
.
令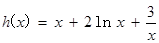 ,遵循“求導(dǎo)數(shù),求駐點(diǎn),討論單調(diào)性,確定最值”.
,遵循“求導(dǎo)數(shù),求駐點(diǎn),討論單調(diào)性,確定最值”.
“表解法”往往直觀易懂,避免出錯(cuò).
試題解析:(Ⅰ)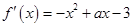 1分
1分
當(dāng)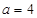 時(shí),
時(shí), 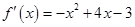 ,令
,令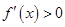 得
得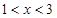 2分
2分
∴當(dāng)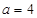 時(shí),
時(shí),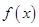 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為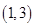 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為 . 3分
. 3分
(Ⅱ)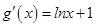 , 令
, 令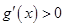 ,得
,得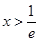 4分
4分
①當(dāng)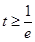 時(shí),在區(qū)間
時(shí),在區(qū)間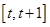 上
上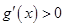 ,
, 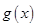 為增函數(shù),
為增函數(shù),
∴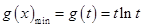 5分
5分
②當(dāng)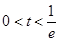 時(shí),在區(qū)間
時(shí),在區(qū)間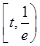 上
上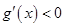 ,
,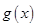 為減函數(shù), 6分
為減函數(shù), 6分
在區(qū)間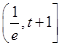 上
上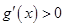 ,
,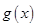 為增函數(shù), 7分
為增函數(shù), 7分
∴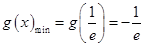 8分
8分
(III) 由 可得
可得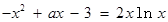
∴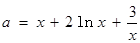 , 9分
, 9分
令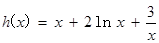 ,則
,則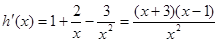 10分
10分