
在等差數列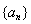 中,
中,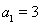 ,其前n項和為
,其前n項和為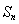 ,等比數列
,等比數列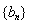 的各項均為正數,
的各項均為正數,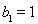 ,公比為q,且
,公比為q,且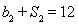 ,
,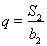 .
.
(1)求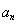 與
與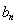 ;
;
(2)設數列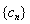 滿足
滿足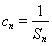 ,求
,求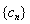 的前n項和
的前n項和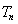 .
.
(1)  ,
, ;(2)
;(2) .
.
【解析】
試題分析:本題主要考查等差數列的通項公式、等比數列的通項公式、等差數列的前n項和公式、裂項相消法求和等數學知識,考查學生的計算能力和分析問題的能力.第一問,利用等比數列的通項公式和等差數列的前n項和公式將已知表達式展開,求出 和
和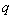 ,從而求出等差數列、等比數列的通項公式;第二問,利用等差數列的前n項和公式先求出
,從而求出等差數列、等比數列的通項公式;第二問,利用等差數列的前n項和公式先求出 ,得到
,得到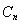 進行裂項,用裂項相消法求數列的前n項和
進行裂項,用裂項相消法求數列的前n項和 .
.
試題解析:(1)設 的公差為
的公差為 .
.
因為 所以
所以 3分
3分
解得  或
或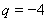 (舍),
(舍),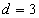
故 ,
, . 6分
. 6分
(2)由(1)可知, , 7分
, 7分
所以 . 9分
. 9分
故 12分
12分
考點:1.等差數列、等比數列的通項公式;2.等差數列的前n項和公式;3.裂項相消法求和.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2011-2012學年甘肅省河西五市高三第二次聯合考試理科數學試卷(解析版) 題型:選擇題
在等差數列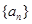 中,
中,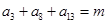 ,其前n項
,其前n項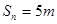 ,則n=
,則n=
A.7 B.8 C.15 D.17
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com