【題目】有3名男生，4名女生，在下列不同要求下，求不同的排列方法種數：
（1）選其中5人排成一排
（2）全體排成一排，甲不站在排頭也不站在排尾
（3）全體排成一排，男生互不相鄰
（4）全體排成一排，甲、乙兩人中間恰好有3人
【答案】（1）2520；（2）3600；（3）1440；（4）720.
【解析】試題分析：
（1）屬于從7個不同元素中任選5個的排列；
（2）第一步先安排特殊元素甲，第二步其他6人全排列即可；
（3）第一步排所有女生，第二步在5個空位（含兩端）排3個男生；
（4）第一步選3人排在甲乙中間（注意這3人全排列），第二步甲乙兩也全排列，第三步甲乙和他們中間的3人作為一個整體與剩下的2人變成3個元素再全排列．
試題解析：
(1)
=2520(種)．
(2)先排甲，有5種方法，其余6人有
種方法，故共有5×=3600(種)．
(3)男生不相鄰，而女生不作要求，∴應先排女生，有
種方法，
再在女生之間及首尾空出的5個空位中任選3個空位排男生，有
種方法，故共有·=1440(種)．
(4)把甲、乙及中間3人看作一個整體，
第一步先排甲、乙兩人有
種方法，
再從剩下的5人中選3人排到中間，有種方法，
最后把甲、乙及中間3人看作一個整體，與剩余2人排列，有
種方法，
故共有··=720(種)．
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的前3項和為6，前8項和為－4.
(1)求數列{an}的通項公式；
(2)設bn＝(4－an)qn－1 (q≠0，n∈N*)，求數列{bn}的前n項和Sn.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】東莞市某高級中學在今年4月份安裝了一批空調，關于這批空調的使用年限
（單位：年， 
）和所支出的維護費用
（單位：萬元）廠家提供的統計資料如下：
（1）請根據以上數據，用最小二乘法原理求出維護費用
關于
的線性回歸方程
；
（2）若規定當維護費用
超過13.1萬元時，該批空調必須報廢，試根據（1）的結論求該批空調使用年限的最大值.
參考公式：最小二乘估計線性回歸方程
中系數計算公式：
， 
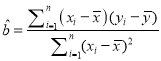查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的離心率為
，且過點
．若點
在橢圓
上，則點
稱為點
的一個“橢點”．
（1）求橢圓
的標準方程；
（2）若直線
： 
與橢圓
相交于
， 
兩點，且
， 
兩點的“橢點”分別為
， 
，以
為直徑的圓經過坐標原點，試求
的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
）在
上的最小值為
，當把
的圖象上所有的點向右平移
個單位后，得到函數
的圖象．
（1）求函數
的解析式；
（2）在△
中，角
，
，
對應的邊分別是
，
，
，若函數
在
軸右側的第一個零點恰為
，
，求△
的面積
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某幼兒園為訓練孩子的數字運算能力，在一個盒子里裝有標號為1,2,3,4,5的卡片各2張，讓孩子從盒子里任取3張卡片，按卡片上最大數字的9倍計分，每張卡片被取出的可能性都相等，用X表示取出的3張卡片上的最大數字
(1)求取出的3張卡片上的數字互不相同的概率；
(2)求隨機變量x的分布列；
(3)若孩子取出的卡片的計分超過30分，就得到獎勵，求孩子得到獎勵的概率
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)的定義域為(－2,2)，函數g(x)＝f(x－1)＋f(3－2x)．
(1)求函數g(x)的定義域；
(2)若f(x)是奇函數，且在定義域上單調遞減，求不等式g(x)≤0的解集．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據以往的經驗，某工程施工期間的降水量
（單位：
）對工期的影響如下表：
降水量 |
|
|
|
|
工期延誤天數 | 0 | 2 | 6 | 10 |
歷年氣象資料表明，該工程施工期間降水量小于300，700，900的概率分別為0.3，0.7，0.9，求：
（1）工期延誤天數
的均值與方差；
（2）在降水量至少是300的條件下，工期延誤不超過6天的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如下圖，在多面體
中，
⊥平面
,
,且
是邊長為2的等邊三角形，
,
與平面
所成角的正弦值為
.
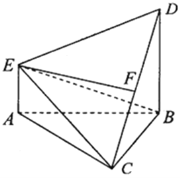
（1）若
是線段的中點，證明：
⊥面
；
（2）求二面角
的平面角的余弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
