【題目】如圖所示，在直三棱柱
中，
，
，其中
為棱
上的中點，
為棱上且位于點上方的動點.
（1）證明：
平面
；
（2）若平面與平面
所成的銳二面角的余弦值為
，求直線
與平面所成角的正弦值.
【答案】（1）見證明；（2）
【解析】
（1）推導出tan∠BB1C=
=
，tan∠PBC=
=，從而∠BB1C=∠PBC，PB⊥B1C，推導出BB1⊥A1B1，A1B1⊥B1C1，從而A1B1⊥平面BCC1B1，A1B1⊥BP，由此能證明BP⊥平面A1B1C．
（2）以BC，BA，BB1為x，y，z軸，建立空間直角坐標系，利用向量法能求出直線BQ與平面A1B1C所成角的正弦值．
（1）證明：在側面
中，因為
，
，
為棱
上的中點，
所以
，
，
所以
，所以
，
在直三棱柱
中，
平面
，
所以
，
因為
，
，所以
，
所以
，
因為
，所以
平面，
所以
，因為
，所以
平面
；
（2）解：如圖，以
，
，
為
軸建立空間直角坐標系，
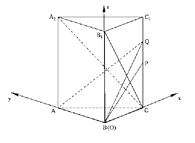
則
，
為平面的一個法向量.
設
，則
，
，
設平面
的法向量為
，則
，
，
所以
，
因為平面與平面所成的銳二面角的余弦值為
，
所以
，所以
，解得，
或
，
由已知得，
，所以，所以
，
所以直線
與平面所成角的正弦值為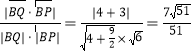
.
期末沖刺100分創新金卷完全試卷系列答案科目：高中數學 來源： 題型：
【題目】橢圓C：
的離心率為
，其右焦點到橢圓C外一點
的距離為
，不過原點O的直線l與橢圓C相交于A，B兩點，且線段AB的長度為2．
1
求橢圓C的方程；
2求
面積S的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有7位歌手（1至7號）參加一場歌唱比賽, 由550名大眾評委現場投票決定歌手名次, 根據年齡將大眾評委分為5組, 各組的人數如下:
組別 | A | B | C | D | E |
人數 | 50 | 100 | 200 | 150 | 50 |
（Ⅰ） 為了調查大眾評委對7位歌手的支持狀況, 現用分層抽樣方法從各組中抽取若干評委, 其中從B組中抽取了6人. 請將其余各組抽取的人數填入下表.
