
【題目】已知等差數列![]() 中,
中, ![]() .等比數列
.等比數列![]() 的通項公式
的通項公式![]() .
.
(I)求數列![]() 的通項公式;
的通項公式;
(II)求數列![]() 的前
的前![]() 項和
項和![]() .
.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】通過研究學生的學習行為,心理學家發現,學生接受能力依賴于老師引入概念和描述問題所用的時間,講座開始時,學生的興趣激增,中間有一段不太長的時間,學生的興趣保持理想的狀態,隨后學生的注意力開始分散,分析結果和實驗表明,用![]() 表示學生掌握和接受概念的能力(
表示學生掌握和接受概念的能力(![]() 的值越大,表示接受能力越強),
的值越大,表示接受能力越強),![]() 表示提出和講授概念的時間(單位:分),可以有以下公式:
表示提出和講授概念的時間(單位:分),可以有以下公式: 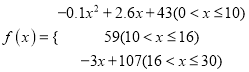 .
.
(1)開講多少分鐘后,學生的接受能力最強?能維持多少分鐘?
(2)開講5分鐘與開講20分鐘比較,學生的接受能力何時強一些?
(3)一個數學難題,需要55的接受能力以及13分鐘的時間,老師能否及時在學生一直達到所需接受能力的狀態下講授完這個難題?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是公差為正數的等差數列,其前
是公差為正數的等差數列,其前![]() 項和為
項和為![]() ,且
,且![]() ,
,![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)數列![]() 滿足
滿足![]() ,
,![]() .
.
①求數列![]() 的通項公式;
的通項公式;
②是否存在正整數![]() ,使得
,使得![]() 成等差數列?若存在,求出
成等差數列?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 中,
中,![]() ,且對任意的
,且對任意的![]() 成等比數列,其公比為
成等比數列,其公比為![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若對任意的![]() 成等差數列,其公差為
成等差數列,其公差為![]() .設
.設![]() .
.
①求證:![]() 成等差數列并指出其公差;
成等差數列并指出其公差;
②若![]() ,試求數列
,試求數列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—5:不等式選講
已知函數f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集為{x|-2≤x≤3},求實數a的值;
(2)在(1)的條件下,若存在實數n使f(n)≤m-f(-n)成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,an+1=![]() ,設bn=
,設bn=![]() ,n∈N*。
,n∈N*。
(1)證明{bn}是等比數列(指出首項和公比);
(2)求數列{log2bn}的前n項和Tn。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某中學高一學生的數學與地理的水平測試成績抽樣統計如下表:若抽取的學生數為![]() ,成績分為
,成績分為![]() (優秀)、
(優秀)、![]() (良好)、
(良好)、![]() (及格)三個等級,設
(及格)三個等級,設![]() ,
, ![]() 分別表示數學成績與地理成績.例如:表中地理成績為
分別表示數學成績與地理成績.例如:表中地理成績為![]() 等級的共有
等級的共有![]() 人,數學成績為
人,數學成績為![]() 級且地理成績為
級且地理成績為![]() 等級的有8人.已知
等級的有8人.已知![]() 與
與![]() 均為
均為![]() 等級的頻率是0.07.
等級的頻率是0.07.
(1)設在該樣本中,數學成績優秀率是![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)已知![]() ,
, ![]() ,求數學成績為
,求數學成績為![]() 等級的人數比數學成績為
等級的人數比數學成績為![]() 等級的人數多的概率.
等級的人數多的概率.
人數
|
|
|
|
| 14 | 40 | 10 |
|
| 36 |
|
| 28 | 8 | 34 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】計劃在某水庫建一座至多安裝3臺發電機的水電站,過去50年的水文資料顯示,水庫年入流量![]() (年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年.將年入流量在以上三段的頻率作為相應段的概率,并假設各年的年入流量相互獨立.
(年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年.將年入流量在以上三段的頻率作為相應段的概率,并假設各年的年入流量相互獨立.
(Ⅰ)求在未來4年中,至多1年的年入流量超過120的概率;
(Ⅱ)水電站希望安裝的發電機盡可能運行,但每年發電機最多可運行臺數受年入流量![]() 限制,并有如下關系;
限制,并有如下關系;
年入流量 |
|
|
|
發電機最多可運行臺數 | 1 | 2 | 3 |
若某臺發電機運行,則該臺發電機年利潤為5000萬元;若某臺發電機未運行,則該臺發電機年虧損800萬元,欲使水電站年總利潤的均值達到最大,應安裝發電機多少臺?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com