
��֪�p����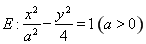 �����Ğ�ԭ�c(di��n)
�����Ğ�ԭ�c(di��n) �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��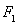 ��
�� ���x���ʞ�
���x���ʞ�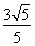 ���c(di��n)
���c(di��n)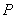 ��ֱ��
��ֱ�� ������һ�c(di��n)���c(di��n)
������һ�c(di��n)���c(di��n)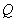 ���p����
���p����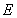 �ϣ��ҝM��
�ϣ��ҝM��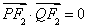 .
.
��1����(sh��)��(sh��)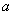 ��ֵ��
��ֵ��
��2���C����ֱ��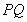 �cֱ��
�cֱ�� ��б��֮�e�Ƕ�ֵ��
��б��֮�e�Ƕ�ֵ��
��3�����c(di��n) �Ŀv����(bi��o)��
�Ŀv����(bi��o)��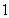 ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)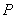 ����(d��ng)ֱ��
����(d��ng)ֱ�� �c�p������֧���ڲ�ͬ�ă��c(di��n)
�c�p������֧���ڲ�ͬ�ă��c(di��n) ��
��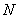 ���ھ���
���ھ���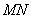 ��ȥ�����c(di��n)
��ȥ�����c(di��n) ��
��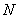 ���c(di��n)
���c(di��n)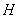 ���M��
���M��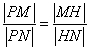 ���C���c(di��n)
���C���c(di��n)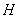 ����һ�l��ֱ����.
����һ�l��ֱ����.
��1��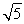 ����2��ԔҊ(ji��n)��������3��ԔҊ(ji��n)����.
����2��ԔҊ(ji��n)��������3��ԔҊ(ji��n)����.
��������
ԇ�}��������1������(j��)�p�������x�����з��������(sh��)��(sh��)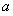 ��ֵ����2���O(sh��)�c(di��n)
��ֵ����2���O(sh��)�c(di��n)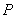 ������(bi��o)��
������(bi��o)��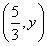 ���c(di��n)
���c(di��n)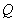 ������(bi��o)��
������(bi��o)��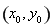 �����×l��
�����×l��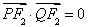 �_��
�_��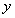 �c
�c ��
��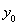 ֮�g���P(gu��n)ϵ���ٽY(ji��)���c(di��n)
֮�g���P(gu��n)ϵ���ٽY(ji��)���c(di��n)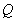 ���p����
���p����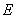 ���@һ�l�����Լ�б�ʹ�ʽ��(l��i)�C��ֱ��
���@һ�l�����Լ�б�ʹ�ʽ��(l��i)�C��ֱ��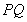 �cֱ��
�cֱ��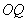 ��б��֮�e�Ƕ�ֵ����3���C��һ�����O(sh��)�c(di��n)
��б��֮�e�Ƕ�ֵ����3���C��һ�����O(sh��)�c(di��n)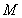 ��
��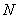 ������(bi��o)�քe��
������(bi��o)�քe�� ��
��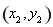 ���Y(ji��)�ϣ�2���õ�
���Y(ji��)�ϣ�2���õ�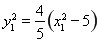 ��
��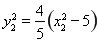 ������?y��n)��?sh��)
������?y��n)��?sh��)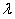 ������
������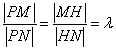 �D(zhu��n)��������(y��ng)�ėl��
�D(zhu��n)��������(y��ng)�ėl�� ����������(bi��o)�\(y��n)��õ��c(di��n)
����������(bi��o)�\(y��n)��õ��c(di��n)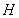 ������(bi��o)���M����P(gu��n)ϵʽ
������(bi��o)���M����P(gu��n)ϵʽ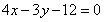 ���M(j��n)���C���c(di��n)
���M(j��n)���C���c(di��n)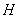 ���ڶ�ֱ��
���ڶ�ֱ��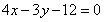 �ϣ��C�������O(sh��)ֱ��
�ϣ��C�������O(sh��)ֱ��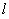 �ķ��̞�
�ķ��̞�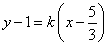 ����ֱ��
����ֱ��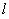 �ķ����c�p�����ķ���(li��n)�����Y(ji��)���f�_(d��)���������l��
�ķ����c�p�����ķ���(li��n)�����Y(ji��)���f�_(d��)���������l��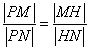 �M(j��n)�еȃr(ji��)�D(zhu��n)����
�M(j��n)�еȃr(ji��)�D(zhu��n)���� ���Y(ji��)���f�_(d��)��������(ji��n)��
���Y(ji��)���f�_(d��)��������(ji��n)��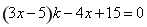 ����������c(di��n)
����������c(di��n)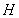 ��ֱ��
��ֱ��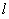 �ϵõ�
�ϵõ�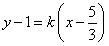 ���Ķ���ȥ
���Ķ���ȥ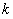 �õ�
�õ�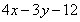
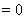 ���M(j��n)���C���c(di��n)
���M(j��n)���C���c(di��n)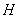 ���ڶ�ֱ��
���ڶ�ֱ��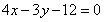 ��.
��.
ԇ�}��������1������(j��)�p�����Ķ��x�ɵ��p�������x���ʞ�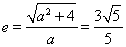 ������
������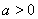 �����
�����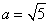 ��
��
���p����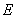 �ķ��̞�
�ķ��̞�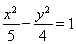 ��
��
��2���O(sh��)�c(di��n)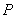 ������(bi��o)��
������(bi��o)��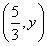 ���c(di��n)
���c(di��n)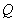 ������(bi��o)��
������(bi��o)��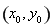 ����֪�c(di��n)
����֪�c(di��n)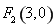 ��
��
�t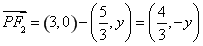 ��
��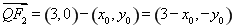 ��
��
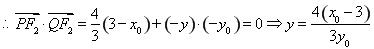 ������c(di��n)
������c(di��n)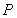 ������(bi��o)��
������(bi��o)�� ��
��
��ֱ��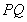 ��б��
��б�� ��ֱ��
��ֱ��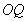 ��б�ʞ�
��б�ʞ�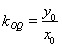 ��
��
���ֱ��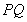 �cֱ��
�cֱ��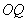 ��б��֮�e��
��б��֮�e��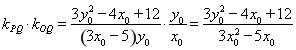 ��
��
�����c(di��n)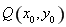 ���p����
���p����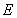 �ϣ�����
�ϣ�����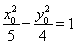 ������
������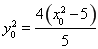 ��
��
������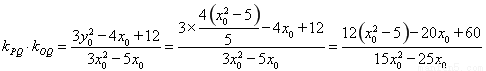
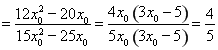 ����ֵ����
����ֵ����
��3���C��һ���O(sh��)�c(di��n)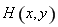 ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)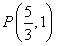 ��ֱ��
��ֱ��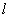 �c�p����
�c�p����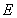 ����֧���ڲ�ͬ�ă��c(di��n)
����֧���ڲ�ͬ�ă��c(di��n)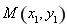 ��
��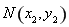 ���ɣ�2��֪��
���ɣ�2��֪��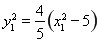 ��
��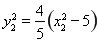 ��
��
�O(sh��)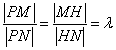 ���t
���t ����
����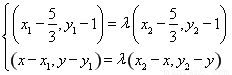 ��
��
������ ��
��
�ɢ� �ۣ���
�ۣ��� �ܵã�
�ܵã� ��
��
��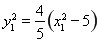 ��
��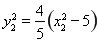 �������
�������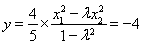 ���ߣ�
���ߣ�
���ߴ���ݵ�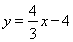 �����c(di��n)
�����c(di��n)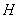 ���ڶ�ֱ��
���ڶ�ֱ��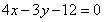 �ϣ�
�ϣ�
�C���������}�⣬ֱ��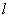 ��б��
��б�� ���ڣ��O(sh��)ֱ��
���ڣ��O(sh��)ֱ��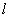 �ķ��̞�
�ķ��̞�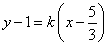 ��
��
�� ��
��
��ȥ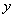 ��
��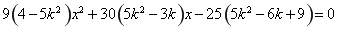 ��
��
��?y��n)�ֱ��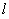 �c�p����
�c�p����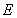 ����֧���ڲ�ͬ�ă��c(di��n)
����֧���ڲ�ͬ�ă��c(di��n)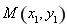 ��
��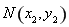 ��
��
�t��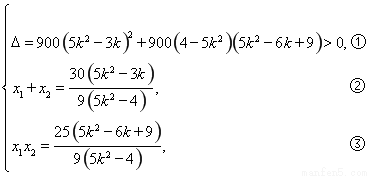 ��
��
�O(sh��)�c(di��n)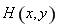 ����
����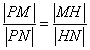 ����
���� ��
��
������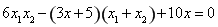 ��
��
���ڢ۴�����ʽ��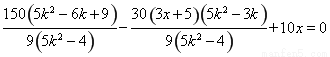 ��
��
������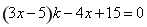 ����
����
��?y��n)��c(di��n)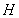 ��ֱ��
��ֱ��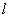 �ϣ�����
�ϣ�����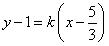 ����
����
(li��n)���ܢ���ȥ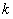 ��
��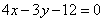 �������c(di��n)
�������c(di��n)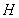 ���ڶ�ֱ��
���ڶ�ֱ��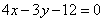 .
.
���c(di��n)��1.�p�������x���ʣ�2.����������(bi��o)�\(y��n)�㣻3.б�ʹ�ʽ��4.�f�_(d��)����


 �(y��ng)���n���n�r(sh��)���I(y��)ϵ�д�
�(y��ng)���n���n�r(sh��)���I(y��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2014��߿���(sh��)�W(xu��)ȫ�̿���(f��)��(x��)�n�r(sh��)�������I(y��)��ʮ����ʮ�µ�ʮ��(ji��)����(x��)���������棩 �}�ͣ��x���}
�P(gu��n)�ھ��Իؚw,�����f(shu��)���e(cu��)�`����(����)
(A)��׃��ȡֵһ���r(sh��),��׃����ȡֵ����һ���S�C(j��)�Եăɂ�(g��)׃��֮�g���P(gu��n)ϵ�������P(gu��n)�P(gu��n)ϵ
(B)��ƽ��ֱ������(bi��o)ϵ�������c(di��n)�ķ����õ��ı�ʾ�������P(gu��n)�P(gu��n)ϵ�ăɂ�(g��)׃����һ�M��(sh��)��(j��)�ĈD�ν���ɢ�c(di��n)�D
(C)���Իؚwֱ���������ܴ����^�y(c��)ֵx,y֮�g���P(gu��n)ϵ,����ؚwֱ��һ���^(gu��)�ӱ������c(di��n)(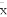 ,
,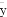 )
)
(D)�ס��ҡ���������λͬ�W(xu��)���Ԍ�(du��)A,B��׃���ľ������P(gu��n)����ԇ�(y��n),���ɻؚw�������քe������P(gu��n)ϵ��(sh��)rxy���±�
| �� | �� | �� | �� |
rxy | 0.82 | 0.78 | 0.69 | 0.85 |
�t��ͬ�W(xu��)��ԇ�(y��n)�Y(ji��)���w�F(xi��n)A,B��׃������(qi��ng)�ľ������P(gu��n)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2014����Д�(sh��)�W(xu��)ȫ��(gu��)��ʡ�����ƌ�(d��o)��(sh��)���x22�����}����(x��)���������棩 �}�ͣ�����}
��֪����(sh��) ��
��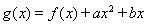 ������(sh��)
������(sh��)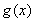 �ĈD�����c(di��n)
�ĈD�����c(di��n)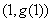 ̎���о�ƽ����
̎���о�ƽ����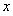 �S��
�S��
��1���_�� �c
�c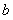 ���P(gu��n)ϵ��
���P(gu��n)ϵ��
��2��ԇӑՓ����(sh��) �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��3���C������(du��)����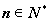 ������
������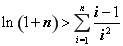 ������
������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2014�����ʡ���(y��ng)�и߿�ģ�M��ԇ��һ�����Ɣ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
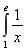 dx +
dx +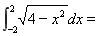 .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2014�����ʡ���(y��ng)�и߿�ģ�M��ԇ��һ�����Ɣ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ��x���}
�� չ�_(k��i)ʽ�д��ڳ���(sh��)�(xi��ng),�tn��ֵ�����ǣ�������
չ�_(k��i)ʽ�д��ڳ���(sh��)�(xi��ng),�tn��ֵ�����ǣ�������
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2014��V�|ʡ�V���Ю��I(y��)��C�Ϝy(c��)ԇһ���Ɣ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
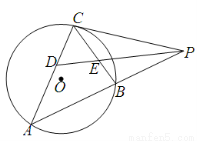
��D��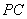 �LjA
�LjA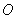 ��������c(di��n)���c(di��n)
���о������c(di��n)���c(di��n)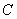 ��ֱ��
��ֱ��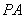 �c�A
�c�A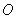 ����
����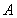 ��
��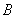 ���c(di��n)��
���c(di��n)��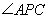 �Ľ�ƽ�־�����
�Ľ�ƽ�־�����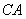 ��
��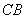 ��
��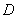 ��
��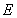 ���c(di��n)����֪
���c(di��n)����֪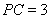 ��
��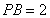 ���t
���t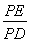 ��ֵ�� .
��ֵ�� .
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2014��V�|ʡ�V���Ю��I(y��)��C�Ϝy(c��)ԇһ���Ɣ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ��x���}
�O(sh��)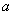 ��
��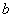 ��
��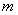 ������(sh��)
������(sh��)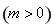 ����
����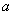 ��
��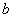 ��
��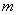 ��������(sh��)��ͬ���t�Q
��������(sh��)��ͬ���t�Q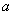 ��
��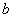 ��(du��)ģ
��(du��)ģ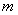 ͬ�࣬ӛ
ͬ�࣬ӛ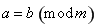 .��
.��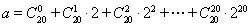 ����
����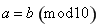 ���t
���t ��ֵ���Ԟ飨 ��
��ֵ���Ԟ飨 ��
A. B.
B.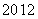 C.
C.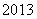 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2014��V�|ʡ�V���Ю��I(y��)��C�Ϝy(c��)ԇһ�ĿƔ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
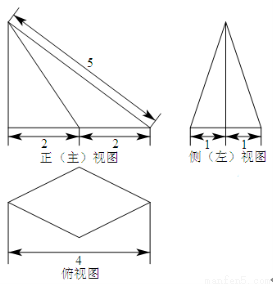
һ��(g��)�����F�ĵ�������Σ�����ҕ�D��D��ʾ���t�@��(g��)�����F���w�e�� .
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2013-2014�W(xu��)�꣨���Ռ��ã��߿���(sh��)�W(xu��)���ģ�����ģ�M��1����(x��)���������棩 �}�ͣ�����}
���タy��x2�ϵ��c(di��n)��ֱ��x��y��1��0����̾��x��________��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com