
【題目】某地區試行高考考試改革:在高三學年中舉行5次統一測試,學生如果通過其中2次測試即可獲得足夠學分升上大學繼續學習,不用參加其余的測試,而每個學生最多也只能參加5次測試![]() 假設某學生每次通過測試的概率都是
假設某學生每次通過測試的概率都是![]() ,每次測試時間間隔恰當,每次測試通過與否互相獨立.
,每次測試時間間隔恰當,每次測試通過與否互相獨立.
(1)求該學生考上大學的概率.
(2)如果考上大學或參加完5次測試就結束,記該生參加測試的次數為X,求X的概率分布及X的數學期望.
科目:高中數學 來源: 題型:
【題目】隨著現代社會的發展,我國對于環境保護越來越重視,企業的環保意識也越來越強.現某大型企業為此建立了5套環境監測系統,并制定如下方案:每年企業的環境監測費用預算定為1200萬元,日常全天候開啟3套環境監測系統,若至少有2套系統監測出排放超標,則立即檢查污染源處理系統;若有且只有1套系統監測出排放超標,則立即同時啟動另外2套系統進行1小時的監測,且后啟動的這2套監測系統中只要有1套系統監測出排放超標,也立即檢查污染源處理系統.設每個時間段(以1小時為計量單位)被每套系統監測出排放超標的概率均為![]() ,且各個時間段每套系統監測出排放超標情況相互獨立.
,且各個時間段每套系統監測出排放超標情況相互獨立.
(1)當![]() 時,求某個時間段需要檢查污染源處理系統的概率;
時,求某個時間段需要檢查污染源處理系統的概率;
(2)若每套環境監測系統運行成本為300元/小時(不啟動則不產生運行費用),除運行費用外,所有的環境監測系統每年的維修和保養費用需要100萬元.現以此方案實施,問該企業的環境監測費用是否會超過預算(全年按9000小時計算)?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三陵錐![]() 中,
中,![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,
,![]() 為正三角形,
為正三角形,![]() 為
為![]() 的中點.
的中點.
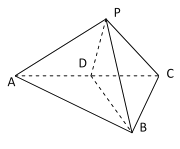
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角為銳角,且棱錐
的平面角為銳角,且棱錐![]() 的體積為
的體積為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】美團外賣和百度外賣兩家公司其“騎手”的日工資方案如下:美團外賣規定底薪70元,每單抽成1元;百度外賣規定底薪100元,每日前45單無抽成,超出45單的部分每單抽成6元,假設同一公司的“騎手”一日送餐單數相同,現從兩家公司個隨機抽取一名“騎手”并記錄其100天的送餐單數,得到如下條形圖:
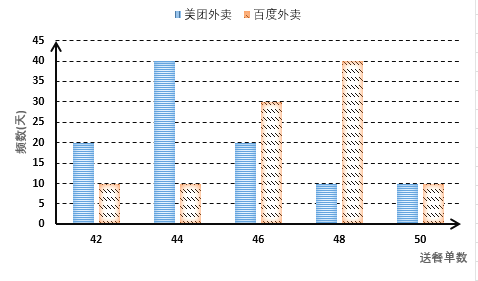
(Ⅰ)求百度外賣公司的“騎手”一日工資![]() (單位:元)與送餐單數
(單位:元)與送餐單數![]() 的函數關系;
的函數關系;
(Ⅱ)若將頻率視為概率,回答下列問題:
①記百度外賣的“騎手”日工資為![]() (單位:元),求
(單位:元),求![]() 的分布列和數學期望;
的分布列和數學期望;
②小明擬到這兩家公司中的一家應聘“騎手”的工作,如果僅從日收入的角度考慮,請你利用所學的統計學知識為他作出選擇,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com