
【題目】設函數f(x)=2cos2x﹣cos(2x﹣![]() ).
).
(1)求f(x)的周期和最大值;
(2)已知△ABC中,角A.B.C的對邊分別為A,B,C,若f(π﹣A)=![]() ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
【答案】(1)周期為π,最大值為2.(2)![]()
【解析】
(1)利用倍角公式降冪,展開兩角差的余弦,將函數的關系式化簡余弦型函數,可求出函數的周期及最值;
(2)由f(π﹣A)![]() ,求解角A,再利用余弦定理和基本不等式求a的最小值.
,求解角A,再利用余弦定理和基本不等式求a的最小值.
(1)函數f(x)=2cos2x﹣cos(2x![]() )
)
=1+cos2x![]()
=cos(2x![]() )+1,
)+1,
∵﹣1≤cos(2x![]() )≤1,
)≤1,
∴T![]() ,f(x)的最大值為2;
,f(x)的最大值為2;
(2)由題意,f(π﹣A)=f(﹣A)=cos(﹣2A![]() )+1
)+1![]() ,
,
即:cos(﹣2A![]() )
)![]() ,
,
又∵0<A<π,
∴![]() 2A
2A![]() ,
,
∴﹣2A![]() ,即A
,即A![]() .
.
在△ABC中,b+c=2,cosA![]() ,
,
由余弦定理,a2=b2+c2﹣2bccosA=(b+c)2﹣bc,
由于:bc![]() ,當b=c=1時,等號成立.
,當b=c=1時,等號成立.
∴a2≥4﹣1=3,即a![]() .
.
則a的最小值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知曲線![]() 為參數),
為參數),![]() 為參數).
為參數).
(1)化![]() 的參數方程為普通方程,并說明它們分別表示什么曲線;
的參數方程為普通方程,并說明它們分別表示什么曲線;
(2)若![]() 上的點
上的點![]() 對應的參數為
對應的參數為![]() 為
為![]() 上的動點,求
上的動點,求![]() 的中點
的中點![]() 到直線
到直線![]() 為參數)距離的最小值.
為參數)距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】求經過直線L1:3x + 4y – 5 = 0與直線L2:2x – 3y + 8 = 0的交點M,且滿足下列條件的直線方程
(1)與直線2x + y + 5 = 0平行 ;
(2)與直線2x + y + 5 = 0垂直;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() ,其中
,其中![]() .函數
.函數![]() 的圖象過點
的圖象過點![]() ,點
,點![]() 與其相鄰的最高點的距離為4.
與其相鄰的最高點的距離為4.
(Ⅰ)求函數![]() 的單調遞減區間;
的單調遞減區間;
(Ⅱ)計算![]() 的值;
的值;
(Ⅲ)設函數![]() ,試討論函數
,試討論函數![]() 在區間 [0,3] 上的零點個數.
在區間 [0,3] 上的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F1 , F2是雙曲線C: ![]() (a>0,b>0)的兩個焦點,P是C上一點,若|PF1|+|PF2|=6a,且△PF1F2的最小內角為30°,則C的離心率為 .
(a>0,b>0)的兩個焦點,P是C上一點,若|PF1|+|PF2|=6a,且△PF1F2的最小內角為30°,則C的離心率為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,將一個各面都涂了油漆的正方體,切割為125個同樣大小的小正方體,經過攪拌后,從中隨機取一個小正方體,記它的涂漆面數為X,則X的均值E(X)=( )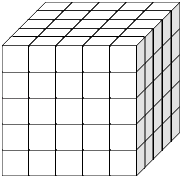
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 已知a1=1, ![]() ,n∈N* .
,n∈N* .
(1)求a2的值;
(2)求數列{an}的通項公式;
(3)證明:對一切正整數n,有 ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com