Question

【題目】已知直線l的參數(shù)方程為 （t為參數(shù)），在直角坐標系xOy中，以O為極點，x軸正半軸為極軸建立極坐標系，曲線M的方程為ρ2（1+sin2θ）=1．
（1）求曲線M的直角坐標方程；
（2）若直線l與曲線M只有一個公共點，求傾斜角α的值．

Answer 1

【答案】
（1）解：曲線M的方程為ρ2（1+sin2θ）=1，

∵ρcosθ=x，ρsinθ=y，ρ2=x2+y2，

∴x2+2y2=1

（2）解：∵直線l的參數(shù)方程為 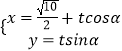（t為參數(shù)），

∴y=tanα（x﹣ ），

由 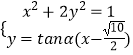，得：x2+2 ，

即（1+2tan2α）x2﹣2 tan2αx+5tan2α﹣1=0，

若直線l與曲線M只有一個公共點，

則△= ﹣4（1+2tan2α）（5tan2α﹣1）=0，

解得：tanα=± ，

∴α= 或

【解析】（1）利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2 ， 進行代換即可得出其直角坐標方程；（2）求出直線l的直角坐標方程，聯(lián)立方程組，根據△=0，得到關于tanα的方程，解出即可．