
【題目】已知函數![]() ,
,![]() .
.
(1)解不等式:![]()
(2)是否存在實數t,使得不等式![]()
![]() ,對任意的
,對任意的![]() 及任意銳角
及任意銳角![]() 都成立,若存在,求出t的取值范圍:若不存在,請說明理由.
都成立,若存在,求出t的取值范圍:若不存在,請說明理由.
【答案】(1)![]() (2)存在,
(2)存在,![]()
【解析】
(1)根據題意,先求出![]() 的解析式,并判斷
的解析式,并判斷![]() 的奇偶性和單調性,結合奇偶性和單調性,即可求解;
的奇偶性和單調性,結合奇偶性和單調性,即可求解;
(2)法一:通過反證法,先假設存在正實數t,使得該不等式對任意的![]() 及任意銳角
及任意銳角![]() 都成立,化簡原不等式,通過推理論證,與
都成立,化簡原不等式,通過推理論證,與![]() 和對任意的
和對任意的![]() 及任意銳角
及任意銳角![]() ,是否矛盾,得出存在
,是否矛盾,得出存在![]() ,且可求出
,且可求出![]() 的取值范圍.
的取值范圍.
法二:先化簡原不等式,通過換元,構造新二次函數![]() ,通過新函數
,通過新函數![]() 恒成立,轉化成二次函數恒成立問題,即可得出存在
恒成立,轉化成二次函數恒成立問題,即可得出存在![]() ,且可求出
,且可求出![]() 的取值范圍.
的取值范圍.
(1)![]() ,
,![]() 為
為![]() 上的奇函數
上的奇函數
又![]() 為R上的增函數
為R上的增函數
于是![]()
![]()
![]()
![]()
故原不等式的解集為![]()
(2)假設存在正實數t,使得該不等式對任意的![]() 及任意銳角
及任意銳角![]() 都成立
都成立
原不等式![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 不等式不可能成立,故
不等式不可能成立,故![]()
![]()
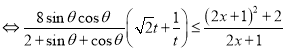
![]()
![]() 不等式對任意的
不等式對任意的![]() 都成立
都成立
![]()
故![]()
而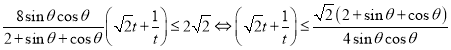
該不等式對任意銳角![]() 都成立
都成立
所以
令![]() ,則
,則
![]()
設![]() ,令
,令![]() ,
,![]()
則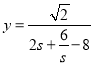 ,而
,而![]() 在
在![]() 單調遞增
單調遞增
故![]()
所以![]() ,即
,即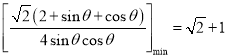
故![]() ,又
,又![]()
![]()
法二:原不等式![]()
![]()
![]()
令![]() ,
,![]()
原不等式
![]()
![]() 時,
時,![]() 不成立,
不成立,![]() 也不可能成立
也不可能成立
故![]()
令![]()
即![]() 恒成立
恒成立
若方程![]() 的
的![]() ,但其兩根和與兩根積都大于0,開口向上
,但其兩根和與兩根積都大于0,開口向上
故![]() 不可能在
不可能在![]() 上恒成立
上恒成立
所以![]() 在
在![]() 上恒成立
上恒成立
![]() 對任意銳角
對任意銳角![]() 恒成立
恒成立
![]()
![]()
同法一可得:![]() .
.


科目:高中數學 來源: 題型:
【題目】已知傾斜角為![]() 的直線
的直線![]() 過點
過點![]() 和點
和點![]() ,點
,點![]() 在第一象限,
在第一象限,![]() .
.
(1)求![]() 的坐標;
的坐標;
(2)若直線![]() 與兩平行直線
與兩平行直線![]() ,
,![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值;
的值;
(3)記集合![]() 直線
直線![]() 經過點
經過點![]() 且與坐標軸圍成的面積為
且與坐標軸圍成的面積為![]() ,
,![]() ,針對
,針對![]() 的不同取值,討論集合
的不同取值,討論集合![]() 中的元素個數.
中的元素個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是水資源匱乏國家,節約用水是每個中國公民應有的意識.為了保護水資源,提倡節約用水,某城市對居民生活用水實行“階梯水價”,計費方法如下表:
每戶每月用水量 | 水價 |
不超過12 | 3元/ |
超過12 | 6元/ |
超過18 | 9元/ |
(1)該城市居民小張家月用水量記為![]() ,應交納水費y(元),試建立y與x的函數解析式,并作出其圖像;
,應交納水費y(元),試建立y與x的函數解析式,并作出其圖像;
(2)若小張家十月份交納水費90元,求他家十月份的用水量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上恰有一個實數解,求
上恰有一個實數解,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若存在
,若存在![]() 使得函數
使得函數![]() 在區間
在區間![]() 上的最大值和最小值的差不超過1,求
上的最大值和最小值的差不超過1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點M(0,2),N(-2,0),直線l:kx-y-2k+2=0(k為常數).
(1)若點M,N到直線l的距離相等,求實數k的值;
(2)對于l上任意一點P,∠MPN恒為銳角,求實數k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com