
【題目】定義[x]表示不超過x的最大整數,例如[2.11]=2,[﹣1.39]=﹣2,執行如下圖所示的程序框圖,則輸出m的值為 ( )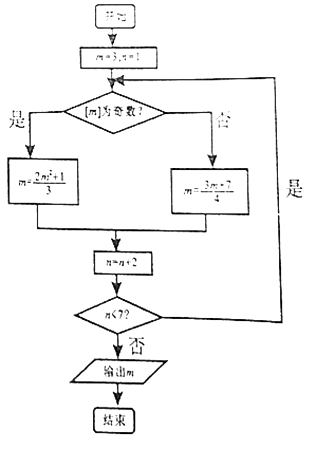
A.![]()
B.![]()
C.![]()
D.![]()
科目:高中數學 來源: 題型:
【題目】已知直線l過點A(0,4),且在兩坐標軸上的截距之和為1.
(Ⅰ)求直線l的方程;
(Ⅱ)若直線l1與直線l平行,且l1與l間的距離為2,求直線l1的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】理科競賽小組有9名女生、12名男生,從中隨機抽取一個容量為7的樣本進行分析.
(Ⅰ)如果按照性別比例分層抽樣,可以得到多少個不同的樣本?(寫出算式即可)
(Ⅱ)如果隨機抽取的7名同學的物理、化學成績(單位:分)對應如表:
學生序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
物理成績 | 65 | 70 | 75 | 81 | 85 | 87 | 93 |
化學成績 | 72 | 68 | 80 | 85 | 90 | 86 | 91 |
規定85分以上(包括85份)為優秀,從這7名同學中再抽取3名同學,記這3名同學中物理和化學成績均為優秀的人數為X,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列![]() 中,已知
中,已知![]() ,對于任意的
,對于任意的![]() ,有
,有![]() .
.
(1)求數列![]() 的通項公式.
的通項公式.
(2)若數列![]() 滿足
滿足![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
(3)設![]() ,是否存在實數
,是否存在實數![]() ,當
,當![]() 時,
時,![]() 恒成立?若存在,求實數
恒成立?若存在,求實數![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是線段BF上一點,AB=AF=BC.
2CE,G是線段BF上一點,AB=AF=BC. 
(Ⅰ)若EG∥平面ABC,求 ![]() 的值;
的值;
(Ⅱ)求二面角A﹣BF﹣E的大小的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年春晚分會場之一是涼山西昌,電視播出后,通過網絡對涼山分會場的表演進行了調查.調查分三類人群進行,參加了網絡調查的觀眾們的看法情況如下:
觀眾對涼山分會場表演的看法 | 非常好 | 好 |
中國人且非四川(人數比例) |
|
|
四川人(非涼山)(人數比例) |
|
|
涼山人(人數比例) |
|
|
(1)從這三類人群中各選一個人,求恰好有2人認為“非常好”的概率(用比例作為相應概率);
(2)若在四川人(非涼山)群中按所持態度分層抽樣,抽取9人,在這9人中任意選取3人,認為“非常好”的人數記為ξ,求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃購買1臺機器,該種機器使用三年后即被淘汰.機器有一易損零件,在購進機器時,可以額外購買這種零件作為備件,每個200元. 在機器使用期間,如果備件不足再購買,則每個500元.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得下面柱狀圖:

記x表示1臺機器在三年使用期內需更換的易損零件數,y表示1臺機器在購買易損零件上所需的費用(單位:元),![]() 表示購機的同時購買的易損零件數.
表示購機的同時購買的易損零件數.
(1)若![]() =19,求y與x的函數解析式;
=19,求y與x的函數解析式;
(2)若要求“需更換的易損零件數不大于![]() ”的頻率不小于0.8,求
”的頻率不小于0.8,求![]() 的最小值;
的最小值;
(3)假設這100臺機器在購機的同時每臺都購買18個易損零件,或每臺都購買19個易損零件,分別計算這100臺機器在購買易損零件上所需費用的平均數,以此作為決策依據,購買1臺機器的同時應購買18個還是19個易損零件?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com