
【題目】若a>b>1,0<c<1,則( )
A.ac<bc
B.abc<bac
C.alogbc<blogac
D.logac<logbc
【答案】C
【解析】解:∵a>b>1,0<c<1,
∴函數f(x)=xc在(0,+∞)上為增函數,故ac>bc , 故A錯誤;
函數f(x)=xc﹣1在(0,+∞)上為減函數,故ac﹣1<bc﹣1 , 故bac<abc , 即abc>bac;故B錯誤;logac<0,且logbc<0,logab<1,
即 ![]() =
= ![]() <1,即logac>logbc.故D錯誤;
<1,即logac>logbc.故D錯誤;
0<﹣logac<﹣logbc,故﹣blogac<﹣alogbc,即blogac>alogbc,即alogbc<blogac,故C正確;
故選:C
根據已知中a>b>1,0<c<1,結合對數函數和冪函數的單調性,分析各個結論的真假,可得答案.本題考查的知識點是不等式的比較大小,熟練掌握對數函數和冪函數的單調性,是解答的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知1是函數f(x)=ax2+bx+c(a>b>c)的一個零點,若存在實數x0.使得f(x0)<0.則f(x)的另一個零點可能是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=x3+ax2+bx+c,下列結論中錯誤的是( )
A. ![]() x0∈R,f (x0)=0
x0∈R,f (x0)=0
B. 函數y=f (x)的圖象是中心對稱圖形
C. 若x0是f (x)的極小值點,則f (x)在區間(∞,x0)上單調遞減
D. 若x0是f (x)的極值點,則f ′(x0)=0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系xOy中,曲線C1的參數方程為 ![]() (α為參數),以坐標原點為極點,以x軸的正半軸為極軸,建立極坐標系,曲線C2的極坐標方程為ρsin(θ+
(α為參數),以坐標原點為極點,以x軸的正半軸為極軸,建立極坐標系,曲線C2的極坐標方程為ρsin(θ+ ![]() )=2
)=2 ![]() .
.
(1)寫出C1的普通方程和C2的直角坐標方程;
(2)設點P在C1上,點Q在C2上,求|PQ|的最小值及此時P的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視傳媒公司為了解某地區觀眾對某體育節目的收視情況,隨機抽取了100名觀眾進行調查,其中女性有55名,下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖:
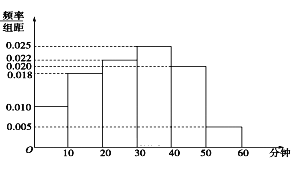
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”.
(1)根據已知條件完成下面的22列聯表,并據此資料你是否認為“體育迷”與性別有關?
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(2)將上述調查所得到的頻率視為概率.現在從該地區大量電視觀眾中,采用隨機抽樣方法每次抽取1名觀眾,抽取3次,記被抽取的3名觀眾中的“體育迷”人數為X.若每次抽取的結果是相互獨立的,求X的分布列,期望E(X)和方差D(X).
附:![]() .
.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某居民區隨機抽取10個家庭,獲得第i個家庭的月收入xi(單位:千元)與月儲蓄yi(單位:千元)的數據資料,算得![]() .
.
(1)求家庭的月儲蓄y對月收入x的線性回歸方程![]() ;
;
(2)判斷變量x與y之間是正相關還是負相關;
(3)若該居民區某家庭月收入為7千元,預測該家庭的月儲蓄.
附:線性回歸方程![]() 中,
中,
,其中![]() 為樣本平均值.
為樣本平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在直角坐標系xOy中,P(1,1),A(x,0)(x>0),B(0,y)(y>0)

(Ⅰ)若x=![]() ,
,![]() ⊥
⊥![]() ,求y的值;
,求y的值;
(Ⅱ)若△OAB的周長為2,求向量![]() 與
與![]() 的夾角.
的夾角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】環境污染已經觸目驚心,環境質量已經成為“十三五”實現全面建成小康社會奮斗目標的短板和瓶頸。綿陽某化工廠每一天中污水污染指數![]() 與時刻
與時刻![]() (時)的函數關系為
(時)的函數關系為![]() 其中
其中![]() 為污水治理調節參數,且
為污水治理調節參數,且![]()
(1)若![]() ,求一天中哪個時刻污水污染指數最低;
,求一天中哪個時刻污水污染指數最低;
(2)規定每天中![]() 的最大值作為當天的污水污染指數,要使該廠每天的污水污染指數不超過
的最大值作為當天的污水污染指數,要使該廠每天的污水污染指數不超過![]() ,則調節參數
,則調節參數![]() 應控制在什么范圍內?
應控制在什么范圍內?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com