一個袋中裝有若干個大小相同的黑球、白球和紅球,已知從袋中任意摸出1個球,得到黑球的概率是
;從袋中任意摸出2個球,至少得到1個白球的概率是
.
(1)若袋中共有10個球,
①求白球的個數;
②從袋中任意摸出3個球,記得到白球的個數為X,求隨機變量X的分布列.
(2)求證:從袋中任意摸出2個球,至少得到1個黑球的概率不大于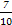
,并指出袋中哪種顏色的球的個數最少.
科目：高中數學 來源： 題型：解答題
設甲、乙、丙三人每次射擊命中目標的概率分別為0.7、0.6和0.5.三人各向目標射擊一次，求至少有一人命中目標的概率及恰有兩人命中目標的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某工廠在試驗階段大量生產一種零件，這種零件有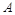
、
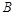兩項技術指標需要檢測，設各項技術指標達標與否互不影響.若有且僅有一項技術指標達標的概率為
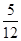，至少一項技術指標達標的概率為
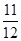．按質量檢驗規定：兩項技術指標都達標的零件為合格品．
（1）求一個零件經過檢測為合格品的概率是多少？
（2）任意依次抽取該種零件4個，設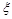
表示其中合格品的個數，求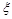的分布列及數學期望
．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
甲、乙等五名大運會志愿者被隨機分到A、B、C、D四個不同的崗位服務，每個崗位至少有一名志愿者．
(1)求甲、乙兩人同時參加A崗位服務的概率；
(2)求甲、乙兩人不在同一崗位服務的概率；
(3)設隨機變量ξ為這五名志愿者中參加A崗位服務的人數，求ξ的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
為了倡導健康、低碳、綠色的生活理念，某市建立了公共自行車服務系統鼓勵市民租用公共自行車出行，公共自行車按每車每次的租用時間進行收費，具體收費標準如下：
①租用時間不超過1小時，免費；
②租用時間為1小時以上且不超過2小時，收費1元；
③租用時間為2小時以上且不超過3小時，收費2元；
④租用時間超過3小時的時段，按每小時2元收費（不足1小時的部分按1小時計算）
已知甲、乙兩人獨立出行，各租用公共自行車一次，兩人租車時間都不會超過3小時，設甲、乙租用時間不超過1小時的概率分別是0.4和0.5;租用時間為1小時以上且不超過2小時的概率分別是0.5和0.3.
（1）求甲、乙兩人所付租車費相同的概率；
（2）設甲、乙兩人所付租車費之和為隨機變量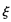
，求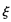的分布列和數學期望E.
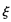查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如圖,在某城市中,M,N兩地之間有整齊的方格形道路網,A1,A2,A3,A4是道路網中位于一條對角線上的4個交匯處,今在道路網M,N處的甲、乙兩人分別要到N,M處,他們分別隨機地選擇一條沿街的最短路徑,同時以每10分鐘一格的速度分別向N,M處行走,直到到達N,M為止.
(1)求甲經過A2的概率.
(2)求甲、乙兩人相遇經A2點的概率.
(3)求甲、乙兩人相遇的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
甲、乙兩人玩一種游戲：在裝有質地、大小完全相同，編號分別為1，2，3，4，5五個球的口袋中，甲先摸出一個球，記下編號，放回后乙再摸一個球，記下編號，如果兩個編號的和為偶數算甲贏，否則算乙贏.
（1）求甲贏且編號和為6的事件發生的概率；
（2）這種游戲規則公平嗎？試說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
甲、乙兩人進行投籃比賽，兩人各投3球，誰投進的球數多誰獲勝，已知每次投籃甲投進的概率為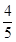
，乙投進的概率為
，求：
(1)甲投進2球且乙投進1球的概率；
(2)在甲第一次投籃未投進的條件下，甲最終獲勝的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
