
【題目】過拋物線![]() 的焦點
的焦點![]() 作直線
作直線![]() 與拋物線交于點
與拋物線交于點![]() 、
、![]() .
.
(1)求證:![]() 不是直角三角形.
不是直角三角形.
(2)當(dāng)![]() 的斜率為
的斜率為![]() 時,拋物線上是否存在點
時,拋物線上是否存在點![]() ,使
,使![]() 為直角三角形?若存在,求出所有的點
為直角三角形?若存在,求出所有的點![]() ;若不存在,說明理由.
;若不存在,說明理由.
【答案】(1)見解析(2)存在4個點![]() ,使
,使![]() 為直角三角形:
為直角三角形: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)如圖,拋物線的焦點為![]() ,
,
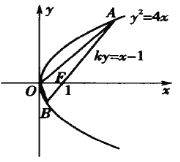
過點![]() 且與拋物線交于點
且與拋物線交于點![]() 、
、![]() 的所有直線可設(shè)為
的所有直線可設(shè)為![]() ,
,
與拋物線![]() 聯(lián)立.消去
聯(lián)立.消去![]() 得
得![]() ,有
,有![]() .
.
進而,![]() .
.
又![]() ,得
,得![]() 為鈍角.
為鈍角.
故![]() 不是直角三角形.
不是直角三角形.
(2)當(dāng)直線![]() 的方程為
的方程為![]() 時,解方程組
時,解方程組![]() ,
,
可得![]() 、
、![]() .
.
假設(shè)拋物線上存在點![]() ,使
,使![]() 為直角三角形,分三種情況討論.
為直角三角形,分三種情況討論.
(i)![]() 為直角.
為直角.
此時,以![]() 為直徑的圓的方程為
為直徑的圓的方程為![]() .
.
把點![]() 、
、![]() 、
、![]() 的坐標(biāo)代入得
的坐標(biāo)代入得
![]() .
.
整理得![]() .
.
因為點![]() 、
、![]() 在圓上,故當(dāng)
在圓上,故當(dāng)![]() 時,必為方程的解.
時,必為方程的解.
注意到![]() ,
,
故方程可分解為![]() .
.
異于點![]() 、
、![]() 的點
的點![]() 必對應(yīng)方程
必對應(yīng)方程![]() 的解,有
的解,有![]() ,
,![]() .
.
故使![]() 的點
的點![]() 有兩個
有兩個![]() ,
,![]() .
.
(ii)![]() 為直角.
為直角.
此時,以![]() 為直徑的圓的方程為
為直徑的圓的方程為![]() .
.
把點![]() 、
、![]() 、
、![]() 的坐標(biāo)代入得
的坐標(biāo)代入得![]() .
.
整理得![]() .
.
解得![]() 對應(yīng)點
對應(yīng)點![]() ,
,![]() 對應(yīng)點
對應(yīng)點![]() .
.
故存在![]() 使
使![]() 為直角三角形.
為直角三角形.
(iii)![]() 為直角.
為直角.
此時,以![]() 為直徑的圓的方程為
為直徑的圓的方程為![]() .
.
把點![]() 、
、![]() 、
、![]() 的坐標(biāo)代入得
的坐標(biāo)代入得![]() .
.
整理得![]() .
.
解得![]() 對應(yīng)點
對應(yīng)點![]() ,
,![]() 對應(yīng)點
對應(yīng)點![]() .
.
故存在![]() 使
使![]() 為直角三角形.
為直角三角形.
綜上知,存在4個點![]() ,使
,使![]() 為直角三角形:
為直角三角形:
![]() ,
,![]() ,
,![]() ,
,![]() .
.


 一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案
一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
極坐標(biāo)系的極點為直角坐標(biāo)系![]() 的原點,極軸為
的原點,極軸為![]() 軸的正半軸,兩種坐標(biāo)系中的長度單位相同,已知曲線
軸的正半軸,兩種坐標(biāo)系中的長度單位相同,已知曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)直線 (
(![]() 為參數(shù))與曲線
為參數(shù))與曲線![]() 交于
交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數(shù)方程為
,其參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù),![]() ,以
,以![]() 為極點,
為極點,![]() 軸非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線
軸非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程
的極坐標(biāo)方程![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)求已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,有點
中,有點![]() 、
、![]() 、
、![]() ,
,![]() 表示
表示![]() 的內(nèi)部及三邊(含頂點)上所有點的集合.試求二元函數(shù)
的內(nèi)部及三邊(含頂點)上所有點的集合.試求二元函數(shù)![]() (點
(點![]() )的取值范圍.
)的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】平面上有7個點,每三點的兩兩連線都組成一個不等邊三角形.求證:一定可以找到4對三角形,使每對三角形的公共邊既是其中一個三角形的最長邊又是另一個三角形的最短邊.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過拋物線![]() 的焦點
的焦點![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點,拋物線在
兩點,拋物線在![]() 處的切線交于
處的切線交于![]() .
.
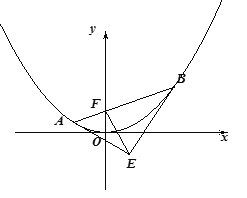
(1)求證:![]() ;
;
(2)設(shè)![]() ,當(dāng)
,當(dāng)![]() 時,求
時,求![]() 的面積
的面積![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某快遞公司收取快遞費用的標(biāo)準(zhǔn)是:重量不超過![]() 的包裹收費
的包裹收費![]() 元;重量超過
元;重量超過![]() 的包裹,除
的包裹,除![]() 收費
收費![]() 元之外,超過
元之外,超過![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 計算)需再收
計算)需再收![]() 元.
元.
該公司將近![]() 天,每天攬件數(shù)量統(tǒng)計如下:
天,每天攬件數(shù)量統(tǒng)計如下:
包裹件數(shù)范圍 |
|
|
|
|
|
包裹件數(shù) (近似處理) |
|
|
|
|
|
天數(shù) |
|
|
|
|
|
(1)某人打算將![]() ,
, ![]() ,
, ![]() 三件禮物隨機分成兩個包裹寄出,求該人支付的快遞費不超過
三件禮物隨機分成兩個包裹寄出,求該人支付的快遞費不超過![]() 元的概率;
元的概率;
(2)該公司從收取的每件快遞的費用中抽取![]() 元作為前臺工作人員的工資和公司利潤,剩余的作為其他費用.前臺工作人員每人每天攬件不超過
元作為前臺工作人員的工資和公司利潤,剩余的作為其他費用.前臺工作人員每人每天攬件不超過![]() 件,工資
件,工資![]() 元,目前前臺有工作人員
元,目前前臺有工作人員![]() 人,那么,公司將前臺工作人員裁員
人,那么,公司將前臺工作人員裁員![]() 人對提高公司利潤是否更有利?
人對提高公司利潤是否更有利?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足a1=1,an+1=an+![]() (c>0,n∈N*),
(c>0,n∈N*),
(Ⅰ)證明:an+1>an≥1;
(Ⅱ)若對任意n∈N*,都有![]() ,證明:(ⅰ)對于任意m∈N*,當(dāng)n≥m時,
,證明:(ⅰ)對于任意m∈N*,當(dāng)n≥m時,![]()
(ⅱ)![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com