
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.
的中點.
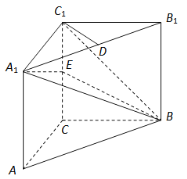
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)見解析(Ⅱ)見解析(Ⅲ)![]()
【解析】
(Ⅰ)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,證明四邊形
,證明四邊形![]() 為平行四邊形后即可得
為平行四邊形后即可得![]() ,再根據線面平行的判定即可得證;
,再根據線面平行的判定即可得證;
(Ⅱ)由等腰三角形的性質和線面垂直的性質可得![]() 、
、![]() ,則可證
,則可證![]() 平面
平面![]() ,再根據面面垂直的判定即可得證;
,再根據面面垂直的判定即可得證;
(Ⅲ)建立空間直角坐標系后,表示出各點坐標,求出平面![]() 的一個法向量為
的一個法向量為![]() ,
,![]() ,利用
,利用![]() 即可得解.
即可得解.
(Ⅰ)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,
因為![]() 是
是![]() 的中點,
的中點,
所以![]() ,且
,且![]() ,
,
在三棱柱![]() 中,
中,
因為![]() 是
是![]() 的中點,所以
的中點,所以![]() ,且
,且![]() ,
,
所以![]() 且
且![]() ,
,
所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
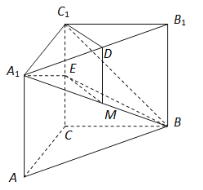
(Ⅱ)證明:因為![]() ,且
,且![]() 是
是![]() 的中點,所以
的中點,所以![]() ,
,
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,
,
又 ![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅲ)如圖建立空間直角坐標系![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則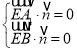 即
即![]() ,
,
令![]() ,則
,則![]() .
.
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
則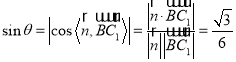 .
.
即直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
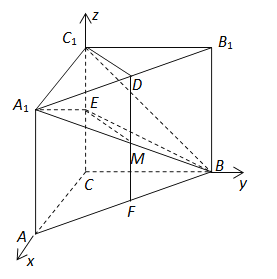


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x-lnx,g(x)=x2-ax.
(1)求函數f(x)在區間[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函數h(x)圖像上任意兩點,且滿足![]() >1,求實數a的取值范圍;
>1,求實數a的取值范圍;
(3)若x∈(0,1],使f(x)≥![]() 成立,求實數a的最大值.
成立,求實數a的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著互聯網金融的不斷發展,很多互聯網公司推出余額增值服務產品和活期資金管理服務產品,如螞蟻金服旗下的“余額寶”,騰訊旗下的“財富通”,京東旗下“京東小金庫”.為了調查廣大市民理財產品的選擇情況,隨機抽取1200名使用理財產品的市民,按照使用理財產品的情況統計得到如下頻數分布表:
分組 | 頻數(單位:名) |
使用“余額寶” |
|
使用“財富通” |
|
使用“京東小金庫” | 30 |
使用其他理財產品 | 50 |
合計 | 1200 |
已知這1200名市民中,使用“余額寶”的人比使用“財富通”的人多160名.
(1)求頻數分布表中![]() ,
,![]() 的值;
的值;
(2)已知2018年“余額寶”的平均年化收益率為![]() ,“財富通”的平均年化收益率為
,“財富通”的平均年化收益率為![]() .若在1200名使用理財產品的市民中,從使用“余額寶”和使用“財富通”的市民中按分組用分層抽樣方法共抽取7人,然后從這7人中隨機選取2人,假設這2人中每個人理財的資金有10000元,這2名市民2018年理財的利息總和為
.若在1200名使用理財產品的市民中,從使用“余額寶”和使用“財富通”的市民中按分組用分層抽樣方法共抽取7人,然后從這7人中隨機選取2人,假設這2人中每個人理財的資金有10000元,這2名市民2018年理財的利息總和為![]() ,求
,求![]() 的分布列及數學期望.注:平均年化收益率,也就是我們所熟知的利息,理財產品“平均年化收益率為
的分布列及數學期望.注:平均年化收益率,也就是我們所熟知的利息,理財產品“平均年化收益率為![]() ”即將100元錢存入某理財產品,一年可以獲得3元利息.
”即將100元錢存入某理財產品,一年可以獲得3元利息.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設三棱錐![]() 的每個頂點都在球
的每個頂點都在球![]() 的球面上,
的球面上,![]() 是面積為
是面積為![]() 的等邊三角形,
的等邊三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
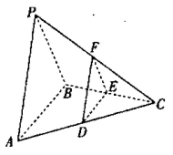
(1)確定![]() 的位置(需要說明理由),并證明:平面
的位置(需要說明理由),并證明:平面![]() 平面
平面![]() .
.
(2)與側面![]() 平行的平面
平行的平面![]() 與棱
與棱![]() ,
,![]() ,
,![]() 分別交于
分別交于![]() ,
,![]() ,
,![]() ,求四面體
,求四面體![]() 的體積的最大值.
的體積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學家劉徽在《九章算術注》中記述:羨除,隧道也,其所穿地,上平下邪.如圖所示的五面體![]() 是一個羨除,兩個梯形側面
是一個羨除,兩個梯形側面![]() 與
與![]() 相互垂直,
相互垂直,![]() .若
.若![]() ,
,![]() ,
,![]() ,梯形
,梯形![]() 與
與![]() 的高分別為3和1,則該羨除的體積
的高分別為3和1,則該羨除的體積![]() ( )
( )
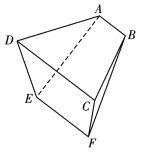
A.3B.4C.5D.6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦點為
的焦點為![]() ,
,![]() ,離心率為
,離心率為![]() ,點P為橢圓C上一動點,且
,點P為橢圓C上一動點,且![]() 的面積最大值為
的面積最大值為![]() ,O為坐標原點.
,O為坐標原點.
(1)求橢圓C的方程;
(2)設點![]() ,
,![]() 為橢圓C上的兩個動點,當
為橢圓C上的兩個動點,當![]() 為多少時,點O到直線MN的距離為定值.
為多少時,點O到直線MN的距離為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·江蘇高考)如圖,在三棱錐ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,點E,F(E與A,D不重合)分別在棱AD,BD上,且EF⊥AD.

求證:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的的參數方程為
的的參數方程為![]() (其中
(其中![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,點
軸的正半軸為極軸的極坐標系中,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 經過點
經過點![]() .曲線
.曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)過點![]() 作直線
作直線![]() 的垂線交曲線
的垂線交曲線![]() 于
于![]() 兩點(
兩點(![]() 在
在![]() 軸上方),求
軸上方),求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com