

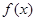 在
在 上為增函數(shù),求正實數(shù)
上為增函數(shù),求正實數(shù)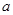 的取值范圍;
的取值范圍; 時,求
時,求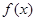 在
在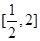 上的最大值和最小值;
上的最大值和最小值; 時,求證:對大于1的任意正整數(shù)
時,求證:對大于1的任意正整數(shù)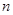 ,都有
,都有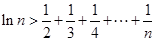 。
。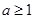 (2)最大值為
(2)最大值為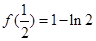 ,最小值為
,最小值為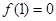 (3)
(3)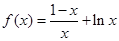 ,
,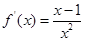
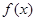 在
在 上為增函數(shù),當
上為增函數(shù),當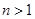 時,令
時,令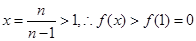
 即
即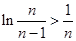 所以
所以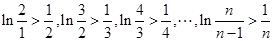
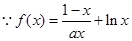 ,
,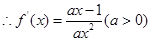
 函數(shù)
函數(shù)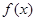 在
在 上為增函數(shù),
上為增函數(shù), 對任意的
對任意的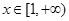 恒成立,
恒成立, 對任意的
對任意的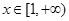 恒成立,即
恒成立,即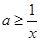 任意的
任意的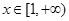 恒成立,…………2分
恒成立,…………2分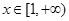 時,
時,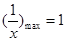 ,
,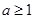 ……………………4分
……………………4分 時,
時,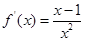
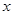 變化時,
變化時,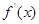 ,
,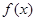 的變化情況如下表
的變化情況如下表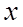 | 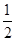 |  | 1 |  | 2 |
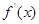 | | 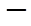 | 0 | 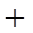 | |
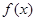 | 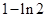 | 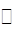 | 0 | 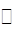 | 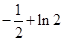 |
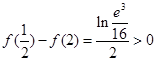
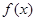 在區(qū)間
在區(qū)間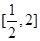 上的最大值為
上的最大值為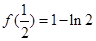 ,最小值為
,最小值為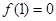 …………8分
…………8分 時,
時,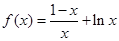 ,
,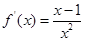 ,
,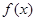 在
在 上為增函數(shù)
上為增函數(shù)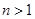 時,令
時,令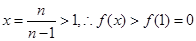
 即
即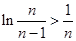 ……………………10分
……………………10分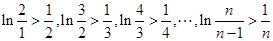
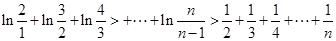
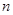 ,都有
,都有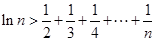 。…………12分
。…………12分

 期末沖刺100分創(chuàng)新金卷完全試卷系列答案
期末沖刺100分創(chuàng)新金卷完全試卷系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
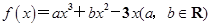 在點
在點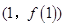 處的切線方程為
處的切線方程為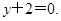
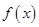 的解析式;
的解析式;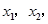 都有
都有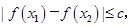 求實數(shù)c的最小值.
求實數(shù)c的最小值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
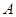 、
、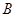 兩個項目,預計投資
兩個項目,預計投資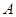 項目
項目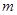 萬元可獲得利潤
萬元可獲得利潤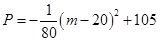
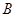 項目
項目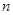 萬元可獲得利潤
萬元可獲得利潤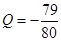
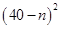
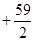
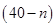 萬元.若該企業(yè)用40
萬元.若該企業(yè)用40查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
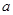 元(一年定期),若年利率為
元(一年定期),若年利率為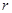 保持不變,且每年到期存款和利息自動轉為新的一年定期,到2012年底將所有存款及利息全部取回,則可取回的錢數(shù)(元)為
保持不變,且每年到期存款和利息自動轉為新的一年定期,到2012年底將所有存款及利息全部取回,則可取回的錢數(shù)(元)為A. | B. | C.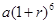 | D.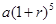 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
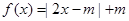 .
.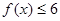 的解集為
的解集為 ,求實數(shù)
,求實數(shù)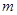 的值;
的值;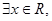 使
使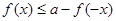 能成立,求實數(shù)a的取值范圍.
能成立,求實數(shù)a的取值范圍.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com