
 .甲方每年受乙方生產影響的經濟損失金額y=0.002t2(元),且乙方每生產一噸產品必須賠付甲方s元(以下s為賠付價格).
.甲方每年受乙方生產影響的經濟損失金額y=0.002t2(元),且乙方每生產一噸產品必須賠付甲方s元(以下s為賠付價格). -st.
-st.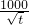 -s=
-s=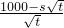 ,
,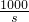 )2.
)2.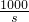 )2(噸);
)2(噸);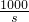 )2(噸);
)2(噸);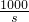 )2代入上式,得到甲方凈收入v與賠付價格s之間的函數關系式v=
)2代入上式,得到甲方凈收入v與賠付價格s之間的函數關系式v=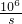 -
-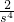 ×109.
×109.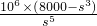 ,
, -st.利用導數法易求出乙方取得最大年利潤的年產量,從而得出乙方獲得最大利潤時的年產t(噸)與賠付價格s(元)滿足的關系式;
-st.利用導數法易求出乙方取得最大年利潤的年產量,從而得出乙方獲得最大利潤時的年產t(噸)與賠付價格s(元)滿足的關系式; .可以得到甲方凈收入v與賠付價格s之間的函數關系式,利用導數法,求出答案.
.可以得到甲方凈收入v與賠付價格s之間的函數關系式,利用導數法,求出答案.

科目:高中數學 來源: 題型:
| t |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com