如圖,已知正方體

棱長為2,
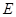
、

、

分別是

、

和

的中點.

(1)證明:

面

;
(2)求二面角

的余弦值.
(1)證明詳見解析;(2)
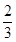
.
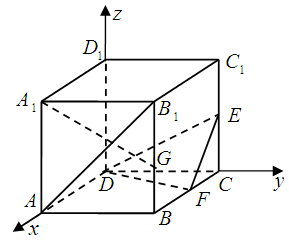
試題分析:先以點
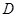
為原點建立空間直角坐標系,然后標明有效點的坐標,(1)寫出有效向量
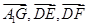
的坐標,利用向量的數(shù)量積為零即可證明
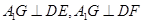
,從而可得

平面

;(2)易知
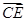
為平面
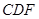
的法向量,先計算
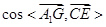
,然后觀察二面角

是銳角還是鈍角,最終確定二面角

的余弦值.
試題解析:以
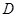
為原點建立如圖空間直角坐標系,正方體棱長為2
則
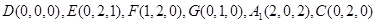
2分
(1)則

,
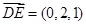
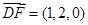
3分
∵
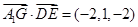
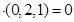
∴
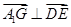
4分
∵
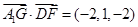

∴
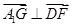
5分
又
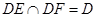
,
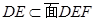
,
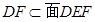
6分
∴

面

7分
(2)由(1)知

為面

的法向量 8分
∵
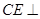
面
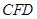
,

為面
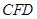
的法向量 9分
設(shè)
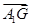
與
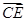
夾角為
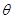
,則
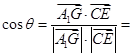
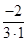
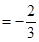
12分
由圖可知二面角

的平面角為
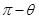
∴二面角

的余弦值為
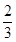
14分.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖所示,正方形AA
1D
1D與矩形ABCD所在平面互相垂直,AB=2AD=2,點E為AB的中點,
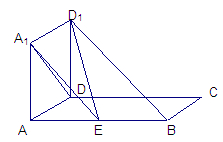
(1).求證:D
1E⊥A
1D;
(2).在線段AB上是否存在點M,使二面角D
1-MC-D的大小為

?,若存在,求出AM的長,若不存在,說明理由
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
直四棱柱

中,底面

為菱形,且

為

延長線上的一點,

面

.設(shè)

.

(Ⅰ)求二面角

的大小;
(Ⅱ)在

上是否存在一點

,使

面

?若存在,求

的值;不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
空間四個不同的平面,它們有多種位置關(guān)系,從交線數(shù)目看,所有可能出現(xiàn)的交線數(shù)目的集合是( )
| A.{0,1,2,3,4,5,6} | B.{0,1,3,4,5,6} |
| C.{0,1,2,3,5,6} | D.{0,1,3,4} |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖所示,在正方體ABCD

A
1B
1C
1D
1中,M、N分別是棱CD、CC
1的中點,則異面直線A
1M與DN所成的角的大小是
.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖,在等腰直角三角形
ABD中,∠
BAD=90°,且等腰直角三角形
ABD與等邊三角形
CBD所在平面垂直,
E為
BC的中點,則
AE與平面
BCD所成角的大小為________.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,正方體

中,

是棱

的中點,

是棱

的中點,則異面直線

與

所成的角為

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,E,F分別是三棱錐

的棱
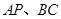
的中點,

,則異面直線AB與PC所成的角為( )

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
邊長為
a的菱形
ABCD中銳角
A=

,現(xiàn)沿對角線
BD折成60°的二面角,翻折后

=
 a
a,則銳角A是( )

查看答案和解析>>

 棱長為2,
棱長為2,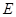 、
、 、
、 分別是
分別是 、
、 和
和 的中點.
的中點.
 面
面 ;
; 的余弦值.
的余弦值.
 ?,若存在,求出AM的長,若不存在,說明理由
?,若存在,求出AM的長,若不存在,說明理由 中,底面
中,底面 為菱形,且
為菱形,且 為
為 延長線上的一點,
延長線上的一點, 面
面 .設(shè)
.設(shè) .
.
 的大小;
的大小;  上是否存在一點
上是否存在一點 ,使
,使 面
面 ?若存在,求
?若存在,求 的值;不存在,說明理由.
的值;不存在,說明理由.