Question

某中學為了解高三年級甲、乙兩班學生的數學學習情況，從兩個班中各隨機抽出10名學生的數學測試成績（單位：分）
甲班：114，135，126，129，122，130，129，123，128，125；
乙班：123，126，128，134，119，120，137，134，119，111．
試估計甲班、乙班學生數學學習情況的期望值和方差（將結果精確到個位），并由此說明哪個班學生的數學成績更整齊．

Answer 1

【答案】分析：利用公式求出兩個樣本的平均數和方差；分析兩個人的成績，作出評價．
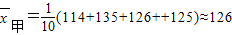
解答：解：∵6（2分）
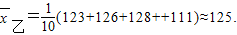
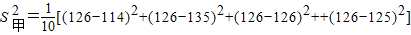
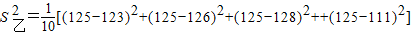
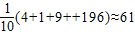
（4分）=（7分）=（10分）
∴甲、乙班學生數學學習情況的期望值分別為126和125；方差分別為29和61
由于，
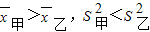
表明甲班的10名學生的數學平均成績比乙班的10名學生的平均成績稍優，而被動小得多，從而估計甲班學生總體數學成績優于乙班，也更整齊．（12分）
點評：本題考查用樣本的平均數、方差來估計總體的平均數、方差，平均數描述了總體的集中趨勢，方差描述其波動大小，屬基礎題，熟記樣本的平均數、方差公式是解答好本題的關鍵．