
��D����֪�����w ��
�� �քe�����(g��)��Č�(du��)�Ǿ���
�քe�����(g��)��Č�(du��)�Ǿ���
��1�����C�� ��
��
��2������ֱ��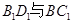 ���ɵĽ�.
���ɵĽ�.
��1����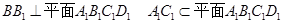 ��
�� ��
�� ���֡�
���֡� ��
�� ��2��
��2��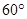
����ԇ�}��������1���������w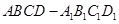 ��.
��.
�� . 1��
. 1��
�� . 2��
. 2��
�֡���߅�� ��������.
��������.
�� . 3��
. 3��
�֡� . 5��
. 5��
�� . 6��
. 6��
��2����
 .
.
����߅�� ��ƽ����߅�Σ���
��ƽ����߅�Σ���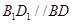 . 8��
. 8��
��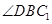 ���Ǯ���ֱ��
���Ǯ���ֱ��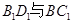 ���ɵĽ�. 9��
���ɵĽ�. 9��
�B��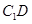 ����
����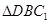 ���߅�����Σ��t
���߅�����Σ��t . 11��
. 11��
�ஐ��ֱ��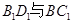 ���ɵĽǞ�
���ɵĽǞ�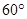 . 12��
. 12��
���c(di��n)�����洹ֱ���ж�������ֱ�����ɽ�
�c(di��n)�u(p��ng)��Ҫ�C���洹ֱ���Cֱ����ֱ��ƽ���(n��i)�ɗl�ֱཻ��������ֱ�����ɽǵIJ��E�����gȡһ�c(di��n)���^(gu��)ԓ�c(di��n)���ɮ���ֱ����ƽ�о����ҵ�����ֱ�����ɽǣ���������εõ������


 ���܌W(xu��)�䑪(y��ng)���}�}��ϵ�д�
���܌W(xu��)�䑪(y��ng)���}�}��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����D��ʾ�Ķ����wABCDE�У�AB��ƽ��ACD��DE��ƽ��ACD��
��AC=AD=CD=DE=2��AB=1��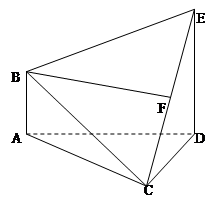
����Ո(q��ng)?ji��n)ھ���CE���ҵ��c(di��n)F��λ�ã�ʹ��ǡ��ֱ��BF��ƽ��ACD�����C���@һ��(sh��)��
����������wABCDE���w�e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D���ڶ����w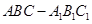 �У���߅��
�У���߅�� �������Σ�
��������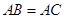 ��
�� ��
��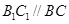 ��
��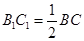 �������
�������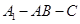 ��ֱ�����
��ֱ�����
��1�����C�� ƽ��
ƽ�� ��
��
��2�����C�� ƽ��
ƽ�� ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D����߅��ABCD�У�AB��AD��AD��BC��AD��6��BC��4��AB��2��E��F�քe��BC��AD�ϣ�EF��AB���F(xi��n)����߅��ABEF��EF����ʹ��ƽ��ABEF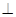 ƽ��EFDC��
ƽ��EFDC��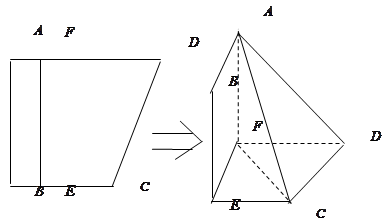
(��) ��(d��ng) ���Ƿ����ۯB���AD�ϴ���һ�c(di��n)
���Ƿ����ۯB���AD�ϴ���һ�c(di��n) ����
���� ��ʹ��CP��ƽ��ABEF�������ڣ����
��ʹ��CP��ƽ��ABEF�������ڣ����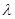 ��ֵ���������ڣ��f(shu��)�����ɣ�
��ֵ���������ڣ��f(shu��)�����ɣ�
(��) �O(sh��)BE��x����(w��n)��(d��ng)x���ֵ�r(sh��)�������FA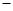 CDF���w�e�����ֵ��������@��(g��)���ֵ��
CDF���w�e�����ֵ��������@��(g��)���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D��AE��ƽ��ABC��AE��BD��AB��BC��CA��BD��2AE��F(xi��n)��CD���c(di��n)��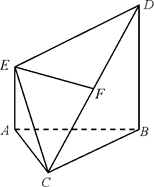
�������C��EF��ƽ��BCD��
����������C��DE��A�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D�����FE��ABCD�У�����ABCD��ƽ����߅�Ρ���ABC=45�㣬BE=BC=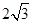 EA=EC=6��M��EC���c(di��n)��ƽ��BCE��ƽ��ACE��AE��EB
EA=EC=6��M��EC���c(di��n)��ƽ��BCE��ƽ��ACE��AE��EB
��I�����C��AE��BC ��II���������FE��ABCD�w�e
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��������ABC-A1B1C1�У���(c��)��ABB1A1����Σ�AB=1��AA1=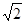 ��D��AA1���c(di��n)��BD�cAB1�����c(di��n)O��CO�A��(c��)��ABB1A1.
��D��AA1���c(di��n)��BD�cAB1�����c(di��n)O��CO�A��(c��)��ABB1A1.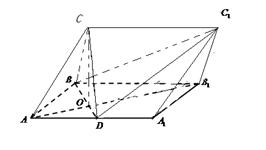
(��)�C����BC�AAB1��
(��)��OC=OA,������C1-BD-C������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D,��֪����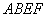 ����ƽ���cֱ������
����ƽ���cֱ������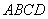 ����ƽ�滥�ഹֱ��
����ƽ�滥�ഹֱ��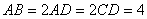 ��
��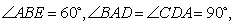 �c(di��n)
�c(di��n) ,
, �քe�Ǿ���
�քe�Ǿ��� ,
, �����c(di��n).
�����c(di��n). 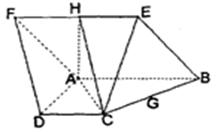
(I)���C��ƽ��
 ƽ��
ƽ�� ;
;
(��)�c(di��n)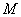 ��ֱ��
��ֱ��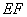 �ϣ���
�ϣ���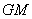 //ƽ��
//ƽ��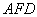 ����ƽ��
����ƽ��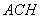 �cƽ��
�cƽ��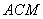 ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�L(zh��ng)���w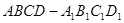 ������
�У�����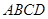 �������Σ�
��������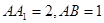 ��
�� ��
�� �ϵ�һ�c(di��n)��
�ϵ�һ�c(di��n)��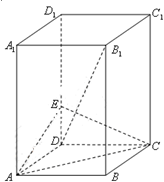
������ֱ��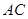 �c
�c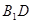 ���ɵĽǣ�
���ɵĽǣ�
����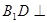 ƽ��
ƽ��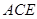 ���������F
���������F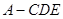 ���w�e��
���w�e��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com