
【題目】已知函數![]() .
.
(1)若![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
,![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(2)在(1)的條件下,求證:![]() .
.
【答案】(1)![]() ;(2)詳見解析.
;(2)詳見解析.
【解析】
(1)由![]() 得
得![]() ,根據
,根據![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
,![]() ,則
,則![]() 有兩個不同的零點,即方程
有兩個不同的零點,即方程![]() 有兩個不同的實根,轉化為直線
有兩個不同的實根,轉化為直線![]() 與
與![]() 的圖象有兩個不同的交點求解.
的圖象有兩個不同的交點求解.
(2)由(1)知![]() ,設
,設![]() ,則
,則![]() ,由
,由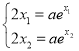 得
得![]() ,
,![]() ,要證
,要證![]() ,將
,將![]() 代入整理為
代入整理為![]() ,再令
,再令![]() ,轉化為
,轉化為![]() ,再構造函數
,再構造函數![]() ,研究其最大值即可.
,研究其最大值即可.
(1)由![]() 得
得![]() ,
,
![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
,![]() ,則
,則![]() 有兩個不同的零點,
有兩個不同的零點,
即方程![]() 有兩個不同的實根,
有兩個不同的實根,
即直線![]() 與
與![]() 的圖象有兩個不同的交點,
的圖象有兩個不同的交點,
設![]() ,則
,則![]() ,
,
![]() 時
時![]() ,
,![]() 單調遞增,且
單調遞增,且![]() 的取值范圍是
的取值范圍是![]() ;
;
![]() 時
時![]() ,
,![]() 單調遞減,且
單調遞減,且![]() 的取值范圍是
的取值范圍是![]() ,
,
所以當![]() 時,直線
時,直線![]() 與
與![]() 的圖象有兩個不同的交點,
的圖象有兩個不同的交點,
![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
,![]() ,
,
故實數![]() 的取值范圍是
的取值范圍是![]() .
.
(2)由(1)知![]() ,設
,設![]() ,則
,則![]() ,
,
由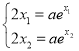 得
得![]() ,
,![]()
所以要證![]() ,只需證
,只需證![]() ,
,
即證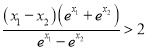 ,即證
,即證![]() ,
,
設![]() ,即證
,即證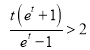 ,即證
,即證![]() ,
,
設![]() ,則
,則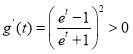 ,
,
所以![]() 在
在![]() 是增函數,
是增函數,![]() ,
,
所以![]() ,從而有
,從而有![]() .
.


科目:高中數學 來源: 題型:
【題目】由甲、乙、丙三個人組成的團隊參加某項闖關游戲,第一關解密碼鎖,3個人依次進行,每人必須在1分鐘內完成,否則派下一個人.3個人中只要有一人能解開密碼鎖,則該團隊進入下一關,否則淘汰出局.根據以往100次的測試,分別獲得甲、乙解開密碼鎖所需時間的頻率分布直方圖.
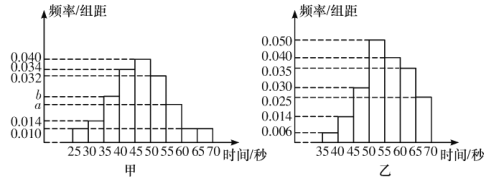
(1)若甲解開密碼鎖所需時間的中位數為47,求![]() 、
、![]() 的值,并分別求出甲、乙在1分鐘內解開密碼鎖的頻率;
的值,并分別求出甲、乙在1分鐘內解開密碼鎖的頻率;
(2)若以解開密碼鎖所需時間位于各區間的頻率代替解開密碼鎖所需時間位于該區間的概率,并且丙在1分鐘內解開密碼鎖的概率為0.5,各人是否解開密碼鎖相互獨立.
①按乙丙甲的先后順序和按丙乙甲的先后順序哪一種可使派出人員數目的數學期望更小.
②試猜想:該團隊以怎樣的先后順序派出人員,可使所需派出的人員數目![]() 的數學期望達到最小,不需要說明理由.
的數學期望達到最小,不需要說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國剩余定理”又稱“孫子定理”,最早可見于中國南北朝時期的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”,原文如下:今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二.問物幾何?現有這樣一個相關的問題:將1到2020這2020個自然數中被5除余3且被7除余2的數按照從小到大的順序排成一列,構成一個數列,則該數列各項之和為( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠連續6天對新研發的產品按事先擬定的價格進行試銷,得到一組數據![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
試銷價 | 9 | 11 | 10 | 12 | 13 | 14 |
產品銷量 | 40 | 32 | 29 | 35 | 44 |
|
(1)試根據4月2日、3日、4日的三組數據,求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測4月6日的產品銷售量
,并預測4月6日的產品銷售量![]() ;
;
(2)若選取兩組數據確定回歸方程,求選取得兩組數據恰好是不相鄰兩天的事件![]() 的概率.
的概率.
參考公式:![]()
其中
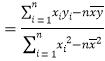 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為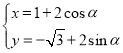 (其中
(其中![]() 為參數,
為參數,![]() ).在極坐標系(以坐標原點
).在極坐標系(以坐標原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸)中,曲線
軸非負半軸為極軸)中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 上恰有一個點到曲線
上恰有一個點到曲線![]() 的距離為1,求曲線
的距離為1,求曲線![]() 的直角坐標方程.
的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() .
.
(1)若數列![]() 的首項為
的首項為![]() ,其中
,其中![]() ,且
,且![]() ,
,![]() ,
,![]() 構成公比小于0的等比數列,求
構成公比小于0的等比數列,求![]() 的值;
的值;
(2)若![]() 是公差為d(d>0)的等差數列
是公差為d(d>0)的等差數列![]() 的前n項和,求
的前n項和,求![]() 的值;
的值;
(3)若![]() ,
,![]() ,且數列
,且數列![]() 單調遞增,數列
單調遞增,數列![]() 單調遞減,求數列
單調遞減,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設中心在原點,焦點在![]() 軸上的橢圓
軸上的橢圓![]() 過點
過點![]() ,且離心率為
,且離心率為![]() .
.![]() 為
為![]() 的右焦點,
的右焦點,![]() 為
為![]() 上一點,
上一點,![]() 軸,
軸,![]() 的半徑為
的半徑為![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直線![]() 與
與![]() 交于
交于![]() 兩點,與
兩點,與![]() 交于
交于![]() 兩點,其中
兩點,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,以
中,以![]() 軸為始邊做兩個銳角
軸為始邊做兩個銳角![]() ,它們的終邊分別與單位圓相交于A,B兩點,已知A,B的橫坐標分別為
,它們的終邊分別與單位圓相交于A,B兩點,已知A,B的橫坐標分別為![]()

(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某人承包了一塊矩形土地![]() 用來種植草莓,其中
用來種植草莓,其中![]() m,
m,![]() m.現規劃建造如圖所示的半圓柱型塑料薄膜大棚
m.現規劃建造如圖所示的半圓柱型塑料薄膜大棚![]() 個,每個半圓柱型大棚的兩半圓形底面與側面都需蒙上塑料薄膜(接頭處忽略不計),塑料薄膜的價格為每平方米
個,每個半圓柱型大棚的兩半圓形底面與側面都需蒙上塑料薄膜(接頭處忽略不計),塑料薄膜的價格為每平方米![]() 元;另外,還需在每個大棚之間留下
元;另外,還需在每個大棚之間留下![]() m寬的空地用于建造排水溝與行走小路(如圖中
m寬的空地用于建造排水溝與行走小路(如圖中![]() m),這部分建設造價為每平方米
m),這部分建設造價為每平方米![]() 元.
元.
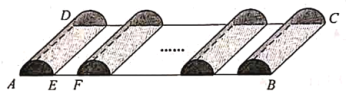
(1)當![]() 時,求蒙一個大棚所需塑料薄膜的面積;(本小題結果保留
時,求蒙一個大棚所需塑料薄膜的面積;(本小題結果保留![]() )
)
(2)試確定大棚的個數,使得上述兩項費用的和最低?(本小題計算中![]() 取
取![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com