
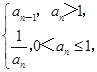 則下列結(jié)論中錯誤的是( )
則下列結(jié)論中錯誤的是( ) A.若m=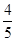 ,則a5=3 ,則a5=3 |
| B.若a3=2,則m可以取3個不同的值 |
C.若m=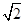 ,則數(shù)列{an}是周期為3的數(shù)列 ,則數(shù)列{an}是周期為3的數(shù)列 |
| D.?m∈Q且m≥2,使得數(shù)列{an}是周期數(shù)列 |
 同步學典一課多練系列答案
同步學典一課多練系列答案 經(jīng)典密卷系列答案
經(jīng)典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案科目:高中數(shù)學 來源:不詳 題型:單選題
|
某少數(shù)民族的刺繡有著悠久的歷史,如圖(1)、(2)、(3)、(4)為她們刺繡最簡單的四個圖案,這些圖案都由小正方形構(gòu)成,小正方形數(shù)越多刺繡越漂亮,現(xiàn)按同樣的規(guī)律刺繡(小正方形的擺放規(guī)律相同),設(shè)第n個圖形包含 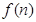 個小正方形.則 個小正方形.則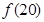 等于( ) 等于( )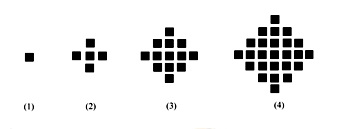
|
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
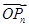 ·OPn+1的最小值;
·OPn+1的最小值;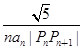 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
| A.a100=-1,S100=5 | B.a100=-3,S100=5 |
| C.a100=-3,S100=2 | D.a100=-1,S100=2 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
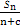 ,求非零常數(shù)c.
,求非零常數(shù)c.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
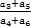 的值為( )
的值為( )A.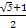 | B. |
C. | D.2 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com