
【題目】如圖,橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,其左焦點(diǎn)到點(diǎn)P(2,1)的距離為
,其左焦點(diǎn)到點(diǎn)P(2,1)的距離為 ![]() ,不過(guò)原點(diǎn)O的直線(xiàn)l與C相交于A,B兩點(diǎn),且線(xiàn)段AB被直線(xiàn)OP平分.
,不過(guò)原點(diǎn)O的直線(xiàn)l與C相交于A,B兩點(diǎn),且線(xiàn)段AB被直線(xiàn)OP平分. 
(1)求橢圓C的方程;
(2)求△APB面積取最大值時(shí)直線(xiàn)l的方程.
【答案】
(1)解:由題意 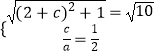 ,解得:
,解得: ![]() .
.
∴所求橢圓C的方程為: ![]() .
.
(2)解:設(shè)A(x1,y1),B(x2,y2),線(xiàn)段AB的中點(diǎn)為M
當(dāng)AB⊥x軸時(shí),直線(xiàn)AB的方程為x=0,與不過(guò)原點(diǎn)的條件不符,故設(shè)AB的方程為y=kx+m(m≠0)
由 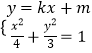 ,消元可得(3+4k2)x2+8kmx+4m2﹣12=0①
,消元可得(3+4k2)x2+8kmx+4m2﹣12=0①
∴ ![]() ,
, ![]()
∴線(xiàn)段AB的中點(diǎn)M ![]()
∵M(jìn)在直線(xiàn)OP上,∴ ![]()
∴k=﹣ ![]()
故①變?yōu)?x2﹣3mx+m2﹣3=0,又直線(xiàn)與橢圓相交,
∴△>0,x1+x2=m, ![]()
∴|AB|= ![]()
P到直線(xiàn)AB的距離d= ![]()
∴△APB面積S= ![]() (m∈(﹣2
(m∈(﹣2 ![]() ,0)
,0) ![]()
令u(m)=(12﹣m2)(m﹣4)2,則 ![]()
∴m=1﹣ ![]() ,u(m)取到最大值
,u(m)取到最大值
∴m=1﹣ ![]() 時(shí),S取到最大值
時(shí),S取到最大值
綜上,所求直線(xiàn)的方程為: ![]()
【解析】(1)由題意,根據(jù)離心率為 ![]() ,其左焦點(diǎn)到點(diǎn)P(2,1)的距離為
,其左焦點(diǎn)到點(diǎn)P(2,1)的距離為 ![]() ,建立方程,即可求得橢圓C的方程;(2)設(shè)A(x1 , y1),B(x2 , y2),線(xiàn)段AB的中點(diǎn)為M,當(dāng)AB⊥x軸時(shí),直線(xiàn)AB的方程為x=0,與不過(guò)原點(diǎn)的條件不符,故設(shè)AB的方程為y=kx+m(m≠0)由
,建立方程,即可求得橢圓C的方程;(2)設(shè)A(x1 , y1),B(x2 , y2),線(xiàn)段AB的中點(diǎn)為M,當(dāng)AB⊥x軸時(shí),直線(xiàn)AB的方程為x=0,與不過(guò)原點(diǎn)的條件不符,故設(shè)AB的方程為y=kx+m(m≠0)由 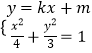 ,消元再利用韋達(dá)定理求得線(xiàn)段AB的中點(diǎn)M,根據(jù)M在直線(xiàn)OP上,可求|AB|,P到直線(xiàn)AB的距離,即可求得△APB面積,從而問(wèn)題得解.
,消元再利用韋達(dá)定理求得線(xiàn)段AB的中點(diǎn)M,根據(jù)M在直線(xiàn)OP上,可求|AB|,P到直線(xiàn)AB的距離,即可求得△APB面積,從而問(wèn)題得解.
【考點(diǎn)精析】關(guān)于本題考查的橢圓的標(biāo)準(zhǔn)方程,需要了解橢圓標(biāo)準(zhǔn)方程焦點(diǎn)在x軸:![]() ,焦點(diǎn)在y軸:
,焦點(diǎn)在y軸:![]() 才能得出正確答案.
才能得出正確答案.


 時(shí)刻準(zhǔn)備著暑假作業(yè)原子能出版社系列答案
時(shí)刻準(zhǔn)備著暑假作業(yè)原子能出版社系列答案 暑假銜接教材期末暑假預(yù)習(xí)武漢出版社系列答案
暑假銜接教材期末暑假預(yù)習(xí)武漢出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了了解我市特色學(xué)校的發(fā)展?fàn)顩r,某調(diào)查機(jī)構(gòu)得到如下統(tǒng)計(jì)數(shù)據(jù):
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
特色學(xué)校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(Ⅰ)根據(jù)上表數(shù)據(jù),計(jì)算![]() 與
與![]() 的相關(guān)系數(shù)
的相關(guān)系數(shù)![]() ,并說(shuō)明
,并說(shuō)明![]() 與
與![]() 的線(xiàn)性相關(guān)性強(qiáng)弱(已知:
的線(xiàn)性相關(guān)性強(qiáng)弱(已知:![]() ,則認(rèn)為
,則認(rèn)為![]() 與
與![]() 線(xiàn)性相關(guān)性很強(qiáng);
線(xiàn)性相關(guān)性很強(qiáng);![]() ,則認(rèn)為
,則認(rèn)為![]() 與
與![]() 線(xiàn)性相關(guān)性一般;
線(xiàn)性相關(guān)性一般;![]() ,則認(rèn)為
,則認(rèn)為![]() 與
與![]() 線(xiàn)性相關(guān)性較弱);
線(xiàn)性相關(guān)性較弱);
(Ⅱ)求![]() 關(guān)于
關(guān)于![]() 的線(xiàn)性回歸方程,并預(yù)測(cè)我市2019年特色學(xué)校的個(gè)數(shù)(精確到個(gè)).
的線(xiàn)性回歸方程,并預(yù)測(cè)我市2019年特色學(xué)校的個(gè)數(shù)(精確到個(gè)).
參考公式: 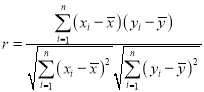 ,
,![]() ,
,![]() ,
,![]() ,
,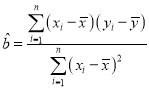 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,側(cè)面
是正方形,側(cè)面![]() ⊥底面
⊥底面![]() ,若
,若![]() 分別為
分別為![]() 的中點(diǎn).
的中點(diǎn).
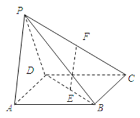
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若函數(shù)![]() 滿(mǎn)足對(duì)任意
滿(mǎn)足對(duì)任意![]() ,都有
,都有![]() 成立,則實(shí)數(shù)
成立,則實(shí)數(shù)![]() 的取值范圍是______.
的取值范圍是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商場(chǎng)經(jīng)營(yíng)一批進(jìn)價(jià)是30元/件的商品,在市場(chǎng)試銷(xiāo)中發(fā)現(xiàn),此商品銷(xiāo)售價(jià)![]() 元與日銷(xiāo)售量
元與日銷(xiāo)售量![]() 件之間有如下關(guān)系:
件之間有如下關(guān)系:
x | 45 | 50 |
y | 27 | 12 |
(1)確定![]() 與
與![]() 的一個(gè)一次函數(shù)關(guān)系式
的一個(gè)一次函數(shù)關(guān)系式![]() ;
;
(2)若日銷(xiāo)售利潤(rùn)為P元,根據(jù)(I)中關(guān)系寫(xiě)出P關(guān)于![]() 的函數(shù)關(guān)系,并指出當(dāng)銷(xiāo)售單價(jià)為多少元時(shí),才能獲得最大的日銷(xiāo)售利潤(rùn)?
的函數(shù)關(guān)系,并指出當(dāng)銷(xiāo)售單價(jià)為多少元時(shí),才能獲得最大的日銷(xiāo)售利潤(rùn)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)某校高三年級(jí)學(xué)生參加社區(qū)服務(wù)次數(shù)進(jìn)行統(tǒng)計(jì),隨機(jī)抽取![]() 名學(xué)生作為樣本,得到這
名學(xué)生作為樣本,得到這![]() 名學(xué)生參加社區(qū)服務(wù)的次數(shù).根據(jù)此數(shù)據(jù)作出了頻數(shù)與頻率的統(tǒng)計(jì)表和頻率分布直方圖:
名學(xué)生參加社區(qū)服務(wù)的次數(shù).根據(jù)此數(shù)據(jù)作出了頻數(shù)與頻率的統(tǒng)計(jì)表和頻率分布直方圖:
分組 | 頻數(shù) | 頻率 |
|
|
|
| 24 |
|
| 4 | 0.1 |
| 2 | 0.05 |
合計(jì) |
| 1 |
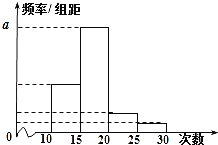
(1)求出表中![]() ,
,![]() 及圖中
及圖中![]() 的值;
的值;
(2)若該校高三學(xué)生有240人,試估計(jì)該校高三學(xué)生參加社區(qū)服務(wù)的次數(shù)在區(qū)間![]() 內(nèi)的人數(shù);
內(nèi)的人數(shù);
(3)在所取樣本中,從參加社區(qū)服務(wù)的次數(shù)不少于20次的學(xué)生中任選2人,求至多一人參加社區(qū)服務(wù)次數(shù)在區(qū)間![]() 內(nèi)的概率.
內(nèi)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)橢圓 ![]() 的左右頂點(diǎn)分別為A,B,點(diǎn)P在橢圓上且異于A,B兩點(diǎn),O為坐標(biāo)原點(diǎn).
的左右頂點(diǎn)分別為A,B,點(diǎn)P在橢圓上且異于A,B兩點(diǎn),O為坐標(biāo)原點(diǎn).
(1)若直線(xiàn)AP與BP的斜率之積為 ![]() ,求橢圓的離心率;
,求橢圓的離心率;
(2)若|AP|=|OA|,證明直線(xiàn)OP的斜率k滿(mǎn)足|k|> ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
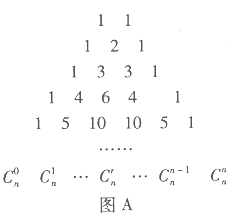
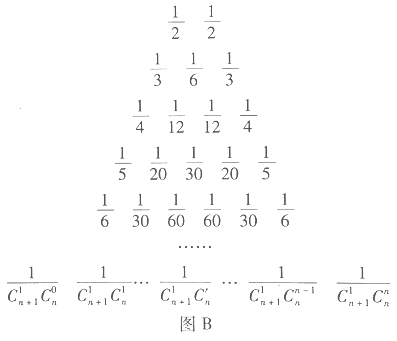
【題目】在我國(guó)南宋數(shù)學(xué)家楊輝所著的《詳解九章算法》(1261年)一書(shū)中,用如圖![]() 所示的三角形,解釋二項(xiàng)和的乘方規(guī)律.在歐洲直到1623年以后,法國(guó)數(shù)學(xué)家布萊士帕斯卡的著作(1655年)介紹了這個(gè)三角形,近年來(lái),國(guó)外也逐漸承認(rèn)這項(xiàng)成果屬于中國(guó),所以有些書(shū)上稱(chēng)這是“中國(guó)三角形”
所示的三角形,解釋二項(xiàng)和的乘方規(guī)律.在歐洲直到1623年以后,法國(guó)數(shù)學(xué)家布萊士帕斯卡的著作(1655年)介紹了這個(gè)三角形,近年來(lái),國(guó)外也逐漸承認(rèn)這項(xiàng)成果屬于中國(guó),所以有些書(shū)上稱(chēng)這是“中國(guó)三角形”![]() ,如圖
,如圖![]() .17世紀(jì)德國(guó)數(shù)學(xué)家萊布尼茨發(fā)現(xiàn)了“萊布尼茨三角形”,如圖
.17世紀(jì)德國(guó)數(shù)學(xué)家萊布尼茨發(fā)現(xiàn)了“萊布尼茨三角形”,如圖![]() .在楊輝三角中,相鄰兩行滿(mǎn)足關(guān)系式:
.在楊輝三角中,相鄰兩行滿(mǎn)足關(guān)系式:![]() ,其 中
,其 中![]() 是行數(shù),
是行數(shù),![]() .請(qǐng)類(lèi)比上式,在萊布尼茨三角形中相鄰兩行滿(mǎn)足的關(guān)系式是__________.
.請(qǐng)類(lèi)比上式,在萊布尼茨三角形中相鄰兩行滿(mǎn)足的關(guān)系式是__________.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com