Question

（19甲）如圖，正三棱柱ABC—A₁B₁C₁的底面邊長為a，側棱長為a

 

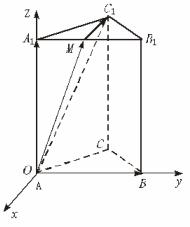
（Ⅰ）建立適當的坐標系，并寫出點A、B、A₁、C₁的坐標；

（Ⅱ）求AC₁與側面ABB₁A₁所成的角.

Answer 1

（19甲）本小題主要考查空間直角坐標系的概念，空間點和向量的坐標表示以及向量夾角的計算方法，考查運用向量研究空間圖形的數學思想方法.

解：

（Ⅰ）如圖，以點A為坐標原點O，以AB所在直線為Oy軸，以AA₁所在直線為Oz軸，以經過原點且與平面ABB₁A₁垂直的直線為Ox軸，建立空間直角坐標系.

由已知，得

A（0，0，0），B（0，a，0），A₁（0，0，a），C₁（－a，，a）.

 

（Ⅱ）坐標系如上，取A₁B₁的中點M，于是有M（0，，a），連AM，MC₁有

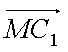 =（－a，0，0），且 =（0，a，0）， =（0，0，a）.

由于·=0，·=0，所以，MC₁⊥面ABB₁A₁.

∴AC₁與AM所成的角就是AC₁與側面ABB₁A₁所成的角.

∵ =（－a，，a），=（0，，a），

∴·=0++2a²=a².                                   

而||==a.

||==a.

∴cos＜，＞==.                                  

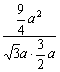所以，與所成的角，即AC₁與側面ABB₁A₁所成的角為30°.