Question

已知直線y=ax+1與雙曲線3x²-y²=1交于不同的兩點A、B.

(1)求實數a的取值范圍.

(2)是否存在這樣的實數a,使A、B兩點關于直線y=x對稱?若存在,求出a的值;若不存在,請說明理由.

Answer 1

思路分析:(1)由于直線與雙曲線交于不同的兩點A、B,利用判別式可確定a的取值范圍,為(2)中判定a值的存在性打下基礎;

(2)點——線——點的對稱問題中,一定要注意應用“垂直且平分”這個條件.

解:(1)由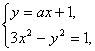得

(3-a²)x²-2ax-2=0.                                                            (*)

由題意可得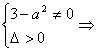-＜a＜,且a≠±.

(2)假設存在實數a,使A、B兩點關于直線y=x對稱,則設A(x₁,y₁)、B(x₂,y₂),

由題意可得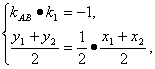

即

∴x₁+x₂=.

設AB的中點為M(x₀,y₀),則x₀=.

又∵點M(x₀,y₀)在直線y=x上,

∴y₀=,即M(,).

又由(1)知x₁+x₂=,

當x₁+x₂=時,求得a=,與a=-2不符.

故不存在實數a使A、B兩點關于直線y=x對稱.