欧美成人一区二区三区四区,一区二区久久精品66国产精品,瑟瑟视频在线免费观看

【題目】直線與圓相交于兩點,當的面積達到最大時,________.

【答案】

【解析】

由圓的方程找出圓心坐標和半徑,同時把直線的方程整理為一般式方程,然后利用點到直線的距離公式表示出圓心到直線的距離,即為圓中弦的弦心距,根據垂徑定理得到垂足為弦的中點,由圓的半徑,弦心距及弦的一半構成的直角三角形,利用勾股定理表示出弦的長度,然后利用三角形的面積公式底乘以高除,用含有的式子表示出三角形的面積,并利用基本不等式求出面積的最大值,以及面積取得最大值時的值,從而列出關于的方程,求出方程的解即可得到面積最大時的值.

解：由圓,

得到圓心坐標為 ,半徑,

把直線的方程為,

整理為一般式方程得：,

.圓心到直線的距離

弦的長度,

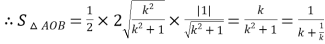又因為,

當且僅當時取等號,取得最大值,最大值為.

解得

故答案為：

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】已知函數

(1)若,求的極值;

(2)若,都有成立,求k的取值范圍.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數，.

（1）證明：在區間上單調遞增；

（2）若存在，使得與在的值域相同，求實數的取值范圍.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】在直角坐標系中，曲線：(為參數)，曲線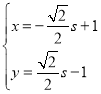：(為參數)，以O為極點，軸的非負半軸為極軸的極坐標系中，已知曲線的極坐標方程為，記曲線與的交點為.

（1）求點的極坐標；

（2）設曲線與相交于A，B兩點，求的值.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】甲、乙兩個商場同時出售一款西門子冰箱，其中甲商場位于老城區中心，乙商場位于高新區.為了調查購買者的年齡與購買冰箱的商場選擇是否具有相關性，研究人員隨機抽取了1000名購買此款冰箱的用戶作調研，所得結果如表所示：

	50歲以上	50歲以下
選擇甲商場	400	250
選擇乙商場	100	250

（1）判斷是否有的把握認為購買者的年齡與購買冰箱的商場選擇具有相關性；

（2）由于乙商場的銷售情況未達到預期標準，商場決定給冰箱的購買者開展返利活動具體方案如下：當天賣出的前60臺（含60臺）冰箱，每臺商家返利200元，賣出60臺以上，超出60臺的部分，每臺返利50元.現將返利活動開展后15天內商場冰箱的銷售情況統計如圖所示：與此同時，老張得知甲商場也在開展返利活動，其日返利額的平均值為11000元，若老張將選擇返利較高的商場購買冰箱，請問老張應當去哪個商場購買冰箱

附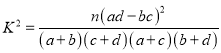：，其中.

	0.100	0.050	0.010	0.001
	2.706	3.841	6.635	10.828

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知橢圓的左、右焦點分別為、，離心率為，點是橢圓上的一個動點，且面積的最大值為.

（1）求橢圓的方程；

（2）過點作直線交橢圓于、兩點，過點作直線的垂線交圓:于另一點.若的面積為3，求直線的斜率.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】關于圓周率，數學發展史上出現過許多有創意的求法，如著名的普豐實驗和查理斯實驗．受其啟發，我們也可以通過設計下面的實驗來估計的值：先請120名同學每人隨機寫下一個x，y都小于1的正實數對，再統計其中x，y能與1構成鈍角三角形三邊的數對的個數m，最后根據統計個數m估計的值．如果統計結果是，那么可以估計的值為（）