
【題目】今年年初,中共中央、國(guó)務(wù)院發(fā)布《關(guān)于開展掃黑除惡專項(xiàng)斗爭(zhēng)的通知》,在全國(guó)范圍部署開展掃黑除惡專項(xiàng)斗爭(zhēng).那么這次的“掃黑除惡”專項(xiàng)斗爭(zhēng)與2000年、2006年兩次在全國(guó)范圍內(nèi)持續(xù)開展了十多年的“打黑除惡”專項(xiàng)斗爭(zhēng)是否相同呢?某高校一個(gè)社團(tuán)在年后開學(xué)后隨機(jī)調(diào)查了![]() 位該校在讀大學(xué)生,就“掃黑除惡”與“打黑除惡”是否相同進(jìn)行了一次調(diào)查,得到具體數(shù)據(jù)如表:
位該校在讀大學(xué)生,就“掃黑除惡”與“打黑除惡”是否相同進(jìn)行了一次調(diào)查,得到具體數(shù)據(jù)如表:
不相同 | 相同 | 合計(jì) | |
男 |
|
|
|
女 |
|
|
|
合計(jì) |
|
|
|
(1)根據(jù)如上的![]() 列聯(lián)表,能否在犯錯(cuò)誤的概率不超過
列聯(lián)表,能否在犯錯(cuò)誤的概率不超過![]() 的前提下,認(rèn)為“掃黑除惡”與“打黑除惡”是否相同與性別有關(guān)"?
的前提下,認(rèn)為“掃黑除惡”與“打黑除惡”是否相同與性別有關(guān)"?
(2)計(jì)算這![]() 位大學(xué)生認(rèn)為“掃黑除惡”與“打黑除惡”不相同的頻率,并據(jù)此估算該校
位大學(xué)生認(rèn)為“掃黑除惡”與“打黑除惡”不相同的頻率,并據(jù)此估算該校![]() 名在讀大學(xué)生中認(rèn)為“掃黑除惡”與“打黑除惡”不相同的人數(shù);
名在讀大學(xué)生中認(rèn)為“掃黑除惡”與“打黑除惡”不相同的人數(shù);
(3)為了解該校大學(xué)生對(duì)“掃黑除惡”與“打黑除惡”不同之處的知道情況,該校學(xué)生會(huì)組織部選取![]() 位男生和
位男生和![]() 位女生逐個(gè)進(jìn)行采訪,最后再隨機(jī)選取
位女生逐個(gè)進(jìn)行采訪,最后再隨機(jī)選取![]() 次采訪記錄放到該大學(xué)的官方網(wǎng)站上,求最后被選取的
次采訪記錄放到該大學(xué)的官方網(wǎng)站上,求最后被選取的![]() 次采訪對(duì)象中至少有一位男生的概率.
次采訪對(duì)象中至少有一位男生的概率.
參考公式:![]()
![]() .
.
附表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)不能在犯錯(cuò)誤的概率不超過![]() 的前提下,認(rèn)為““掃黑除惡”與“打黑除惡”是否相同與性別有關(guān)”;(2)
的前提下,認(rèn)為““掃黑除惡”與“打黑除惡”是否相同與性別有關(guān)”;(2)![]() 人;(3)
人;(3)![]() 。
。
【解析】
(1)計(jì)算觀測(cè)值k2,即可得出結(jié)論;(2)由圖表中的數(shù)據(jù)計(jì)算不相同的頻率, 據(jù)此估算該校![]() 名在讀大學(xué)生不相同的人數(shù);(3)根據(jù)古典概型求概率的方法即可求出.
名在讀大學(xué)生不相同的人數(shù);(3)根據(jù)古典概型求概率的方法即可求出.
(1)根據(jù)列聯(lián)表中的數(shù)據(jù),得到![]() 的觀測(cè)值為
的觀測(cè)值為![]()
故不能在犯錯(cuò)誤的概率不超過![]() 的前提下,認(rèn)為““掃黑除惡”與“打黑除惡”是否相同與性別有關(guān)”。
的前提下,認(rèn)為““掃黑除惡”與“打黑除惡”是否相同與性別有關(guān)”。
(2)這![]() 位大學(xué)生認(rèn)為“掃黑除惡”與“打黑除惡”不相同的頻率為
位大學(xué)生認(rèn)為“掃黑除惡”與“打黑除惡”不相同的頻率為![]()
據(jù)此估算該校![]() 名在讀大學(xué)生中認(rèn)為“掃黑除惡”與“打黑除惡”不相同的人數(shù)為
名在讀大學(xué)生中認(rèn)為“掃黑除惡”與“打黑除惡”不相同的人數(shù)為![]() .
.
(3)設(shè)選取的![]() 位男生和
位男生和![]() 位女生分別記為
位女生分別記為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,隨機(jī)選取
,隨機(jī)選取![]() 次采訪的所有結(jié)果
次采訪的所有結(jié)果
為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共有10個(gè)基本事件,
共有10個(gè)基本事件,
至少有一位男生的基本事件有![]() 個(gè),故所求概率為
個(gè),故所求概率為![]()


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某家庭記錄了未使用節(jié)水龍頭50天的日用水量數(shù)據(jù)(單位:m3)和使用了節(jié)水龍頭50天的日用水量數(shù)據(jù),得到頻數(shù)分布表如下:
未使用節(jié)水龍頭50天的日用水量頻數(shù)分布表
日用 水量 |
|
|
|
|
|
|
|
頻數(shù) | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節(jié)水龍頭50天的日用水量頻數(shù)分布表
日用 水量 |
|
|
|
|
|
|
頻數(shù) | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答題卡上作出使用了節(jié)水龍頭50天的日用水量數(shù)據(jù)的頻率分布直方圖:
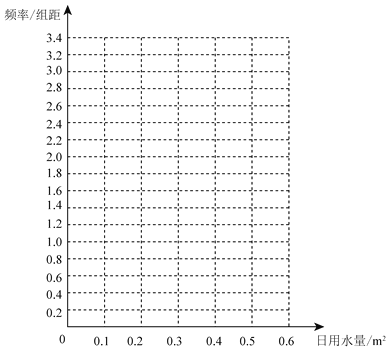
(2)估計(jì)該家庭使用節(jié)水龍頭后,日用水量小于0.35 m3的概率;
(3)估計(jì)該家庭使用節(jié)水龍頭后,一年能節(jié)省多少水?(一年按365天計(jì)算,同一組中的數(shù)據(jù)以這組數(shù)據(jù)所在區(qū)間中點(diǎn)的值作代表.)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的兩個(gè)焦點(diǎn)坐標(biāo)分別是
的兩個(gè)焦點(diǎn)坐標(biāo)分別是![]() 、
、![]() ,并且經(jīng)過點(diǎn)
,并且經(jīng)過點(diǎn)![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() :
:![]() 相切,并與橢圓
相切,并與橢圓![]() 交于不同的兩點(diǎn)
交于不同的兩點(diǎn)![]() 、
、![]() .當(dāng)
.當(dāng)![]() ,且滿足
,且滿足![]() 時(shí),求
時(shí),求![]() 面積
面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知一圓經(jīng)過點(diǎn)![]() ,
,![]() ,且它的圓心在直線
,且它的圓心在直線![]() 上.
上.
(I)求此圓的方程;
(II)若點(diǎn)![]() 為所求圓上任意一點(diǎn),且點(diǎn)
為所求圓上任意一點(diǎn),且點(diǎn)![]() ,求線段
,求線段![]() 的中點(diǎn)
的中點(diǎn)![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《九章算木》中將底面為長(zhǎng)方形,且有一條側(cè)棱與底面垂直的四棱錐稱之為“陽馬”,現(xiàn)有一陽馬,其正視圖和側(cè)視圖是如圖所示的直角三角形,該“陽馬”的體積為![]() ,若該陽馬的頂點(diǎn)都在同一個(gè)球面上,則該球的表面積為( )
,若該陽馬的頂點(diǎn)都在同一個(gè)球面上,則該球的表面積為( )

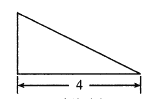
正視圖 側(cè)視圖
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知極點(diǎn)與直角坐標(biāo)系原點(diǎn)重合,極軸與x軸的正半軸重合,圓C的極坐標(biāo)方程為![]() ,直線l的參數(shù)方程為
,直線l的參數(shù)方程為 為參數(shù)
為參數(shù)![]() .
.
![]() 若
若![]() ,直線l與x軸的交點(diǎn)為M,N是圓C上一動(dòng)點(diǎn),求
,直線l與x軸的交點(diǎn)為M,N是圓C上一動(dòng)點(diǎn),求![]() 的最小值;
的最小值;
![]() 若直線l被圓C截得的弦長(zhǎng)等于圓C的半徑,求a的值.
若直線l被圓C截得的弦長(zhǎng)等于圓C的半徑,求a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】規(guī)定![]() ,其中
,其中![]() ,
,![]() 是正整數(shù),且
是正整數(shù),且![]() ,這是組合數(shù)
,這是組合數(shù)![]() (
(![]() 、
、![]() 是正整數(shù),且
是正整數(shù),且![]() )的一種推廣.
)的一種推廣.
(1)求![]() 的值;
的值;
(2)設(shè)![]() ,當(dāng)
,當(dāng)![]() 為何值時(shí),
為何值時(shí),![]() 取得最小值?
取得最小值?
(3)組合數(shù)的兩個(gè)性質(zhì):①![]() .②
.②![]() .是否都能推廣到
.是否都能推廣到![]() (
(![]() ,
,![]() 是正整數(shù))的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由.
是正整數(shù))的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某城市![]() 戶居民的月平均用電量(單位:度),以
戶居民的月平均用電量(單位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖.
分組的頻率分布直方圖如圖.

(1)求直方圖中![]() 的值;
的值;
(2)求月平均用電量的眾數(shù)和中位數(shù);
(3)在月平均用電量為![]() ,
,![]() ,
,![]() ,
,![]() 的四組用戶中,用分層抽樣的方法抽取
的四組用戶中,用分層抽樣的方法抽取![]() 戶居民,則月平均用電量在
戶居民,則月平均用電量在![]() 的用戶中應(yīng)抽取多少戶?
的用戶中應(yīng)抽取多少戶?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“克拉茨猜想”又稱“![]() 猜想”,是德國(guó)數(shù)學(xué)家洛薩克拉茨在1950年世界數(shù)學(xué)家大會(huì)上公布的一個(gè)猜想:任給一個(gè)正整數(shù)
猜想”,是德國(guó)數(shù)學(xué)家洛薩克拉茨在1950年世界數(shù)學(xué)家大會(huì)上公布的一個(gè)猜想:任給一個(gè)正整數(shù)![]() ,如果
,如果![]() 是偶數(shù),就將它減半;如果
是偶數(shù),就將它減半;如果![]() 為奇數(shù)就將它乘3加1,不斷重復(fù)這樣的運(yùn)算,經(jīng)過有限步后,最終都能夠得到1.己知正整數(shù)
為奇數(shù)就將它乘3加1,不斷重復(fù)這樣的運(yùn)算,經(jīng)過有限步后,最終都能夠得到1.己知正整數(shù)![]() 經(jīng)過6次運(yùn)算后得到1,則
經(jīng)過6次運(yùn)算后得到1,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com