
【題目】近年來,隨著“霧霾”天出現的越來越頻繁,很多人為了自己的健康,外出時選擇戴口罩,在一項對人們霧霾天外出時是否戴口罩的調查中,共調查了![]() 人,其中女性
人,其中女性![]() 人,男性
人,男性![]() 人,并根據統計數據畫出等高條形圖如圖所示:
人,并根據統計數據畫出等高條形圖如圖所示:
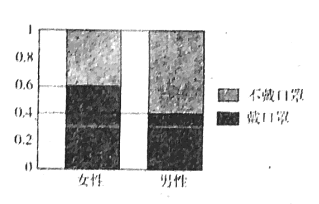
(1)利用圖形判斷性別與霧霾天外出戴口罩是否有關系并說明理由;
(2)根據統計數據建立一個![]() 列聯表;
列聯表;
(3)能否在犯錯誤的概率不超過![]() 的前提下認為性別與霧霾天外出戴口罩的關系.
的前提下認為性別與霧霾天外出戴口罩的關系.
附: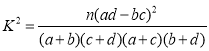
|
|
|
|
|
|
|
|
|
|
【答案】(1)圖形見解析,理由見解析;(2)見解析;(3)犯錯誤的概率不超過![]() 的前提下認為性別與霧霾天外出戴口罩有關系
的前提下認為性別與霧霾天外出戴口罩有關系
【解析】
(1)利用等高條形圖中兩個深顏色條的高比較得出性別與霧霾天外出戴口罩有關系;
(2)填寫![]() 列聯表即可;
列聯表即可;
(3)由表中數據,計算觀測值,對照臨界值得出結論.
解:(1)在等高條形圖中,兩個深色條的高分別表示女性和男性中霧霾天外出戴口罩的頻率,比較圖中兩個深色條的高可以發現,女性中霧霾天外出帶口罩的頻率明顯高于男性中霧霾天外出帶口罩的頻率,因此可以認為性別與霧霾天外出帶口罩有關系.
(2)![]() 列聯表如下:
列聯表如下:
戴口罩 | 不戴口罩 | 合計 | |
女性 |
|
|
|
男性 |
|
|
|
合計 |
|
|
|
(3)由(2)中數據可得:![]() .
.
所以,在犯錯誤的概率不超過的前提下認為性別與霧霾天外出戴口罩有關系.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分10分)選修4-5:不等式選講
已知函數f(x)=log2(|x+1|+|x﹣2|﹣m).
(1)當m=7時,求函數f(x)的定義域;
(2)若關于x的不等式f(x)≥2的解集是R,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某客戶考察了一款熱銷的凈水器,使用壽命為十年,改款凈水器為三級過濾,每一級過濾都由核心部件濾芯來實現.在使用過程中,一級濾芯需要不定期更換,其中每更換![]() 個一級濾芯就需要更換
個一級濾芯就需要更換![]() 個二級濾芯,三級濾芯無需更換.其中一級濾芯每個
個二級濾芯,三級濾芯無需更換.其中一級濾芯每個![]() 元,二級濾芯每個
元,二級濾芯每個![]() 元.記一臺凈水器在使用期內需要更換的二級濾芯的個數構成的集合為
元.記一臺凈水器在使用期內需要更換的二級濾芯的個數構成的集合為![]() .如圖是根據
.如圖是根據![]() 臺該款凈水器在十年使用期內更換的一級濾芯的個數制成的柱狀圖.
臺該款凈水器在十年使用期內更換的一級濾芯的個數制成的柱狀圖.
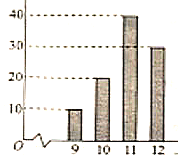
(1)結合圖,寫出集合![]() ;
;
(2)根據以上信息,求出一臺凈水器在使用期內更換二級濾芯的費用大于![]() 元的概率(以
元的概率(以![]() 臺凈水器更換二級濾芯的頻率代替
臺凈水器更換二級濾芯的頻率代替![]() 臺凈水器更換二級濾芯發生的概率);
臺凈水器更換二級濾芯發生的概率);
(3)若在購買凈水器的同時購買濾芯,則濾芯可享受![]() 折優惠(使用過程中如需再購買無優惠).假設上述
折優惠(使用過程中如需再購買無優惠).假設上述![]() 臺凈水器在購機的同時,每臺均購買
臺凈水器在購機的同時,每臺均購買![]() 個一級濾芯、
個一級濾芯、![]() 個二級濾芯作為備用濾芯(其中
個二級濾芯作為備用濾芯(其中![]() ,
,![]() ),計算這
),計算這![]() 臺凈水器在使用期內購買濾芯所需總費用的平均數.并以此作為決策依據,如果客戶購買凈水器的同時購買備用濾芯的總數也為
臺凈水器在使用期內購買濾芯所需總費用的平均數.并以此作為決策依據,如果客戶購買凈水器的同時購買備用濾芯的總數也為![]() 個,則其中一級濾芯和二級濾芯的個數應分別是多少?
個,則其中一級濾芯和二級濾芯的個數應分別是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校需要從甲、乙兩名學生中選一人參加數學競賽,抽取了近期兩人![]() 次數學考試的成績,統計結果如下表:
次數學考試的成績,統計結果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成績(分) |
|
|
|
|
|
乙的成績(分) |
|
|
|
|
|
(1)若從甲、乙兩人中選出一人參加數學競賽,你認為選誰合適?請說明理由.
(2)若數學競賽分初賽和復賽,在初賽中有兩種答題方案:
方案一:每人從![]() 道備選題中任意抽出
道備選題中任意抽出![]() 道,若答對,則可參加復賽,否則被淘汰.
道,若答對,則可參加復賽,否則被淘汰.
方案二:每人從![]() 道備選題中任意抽出
道備選題中任意抽出![]() 道,若至少答對其中
道,若至少答對其中![]() 道,則可參加復賽,否則被潤汰.
道,則可參加復賽,否則被潤汰.
已知學生甲、乙都只會![]() 道備選題中的
道備選題中的![]() 道,那么你推薦的選手選擇哪種答題方條進人復賽的可能性更大?并說明理由.
道,那么你推薦的選手選擇哪種答題方條進人復賽的可能性更大?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,
,![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,
,![]() ,且
,且![]() ,
,![]() 為等邊三角形,過點
為等邊三角形,過點![]() 的直線與橢圓
的直線與橢圓![]() 在
在![]() 軸右側的部分交于
軸右側的部分交于![]() 、
、![]() 兩點.
兩點.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,現以極點
,現以極點![]() 為原點,極軸為
為原點,極軸為![]() 軸的非負半軸建立平面直角坐標系,曲線
軸的非負半軸建立平面直角坐標系,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)求直線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)若曲線![]() 為曲線
為曲線![]() 關于直線
關于直線![]() 的對稱曲線,點
的對稱曲線,點![]() ,
,![]() 分別為曲線
分別為曲線![]() 、曲線
、曲線![]() 上的動點,點
上的動點,點![]() 坐標為
坐標為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過橢圓右焦點
,過橢圓右焦點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,當直線
兩點,當直線![]() 與
與![]() 軸垂直時,
軸垂直時,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)當直線![]() 與
與![]() 軸不垂直時,在
軸不垂直時,在![]() 軸上是否存在一點
軸上是否存在一點![]() (異于點
(異于點![]() ),使
),使![]() 軸上任意點到直線
軸上任意點到直線![]() ,
,![]() 的距離均相等?若存在,求
的距離均相等?若存在,求![]() 點坐標;若不存在,請說明理由.
點坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com