【題目】已知圓C:x2+y2=12,直線l:4x+3y=25,設點A是圓C上任意一點,求點A到直線l的距離小于2的概率.
【答案】
.
【解析】
試題分析：首先與直線l:4x+3y=25平行且到該直線的距離為2的直線為l',且l'與圓C交于P,Q兩點. 可求|PQ|=2
,則∠POQ=
，然后利用幾何概型的公式即可求得本題答案.
試題解析：由x2+y2=12知,圓心為O(0,0),
∴圓心到直線l的距離d=
=5,
如圖所示,設與直線l:4x+3y=25平行且到該直線的距離為2的直線為l',且l'與圓C交于P,Q兩點.
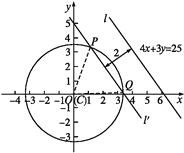
因此點O(0,0)到l'的距離為3,又圓C的半徑r=2,
∴在△POQ中,可求|PQ|=2,則∠POQ=.
設“點A到直線l的距離小于2”為事件M,則事件M發生即點A在劣弧
上.
∵劣弧的長為
,∴P(M)=
.
智慧小復習系列答案科目：高中數學 來源： 題型：
【題目】數列
的前
項和為
，
．
（
）證明數列
是等比數列，求出數列的通項公式．
（
）設
，求數列
的前項和
．
（
）數列中是否存在三項，它們可以構成等比數列？若存在，求出一組符合條件的項；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
.
（1）當
時，求函數
的最大值；
（2）令
，其圖象上存在一點
，使此處切線的斜率
，求實數
的取值范圍；
（3）當
， 
時，方程
有唯一實數解，求正數
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正方形
的中心為點
, 
邊所在的直線方程為
.
（1）求
邊所在的直線方程和正方形
外接圓的方程；
（2）若動圓
過點
,且與正方形
外接圓外切,求動圓圓心
的軌跡方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線
所圍成封閉圖形面積為
,曲線
是以曲線
與坐標軸的交點為頂點的橢圓, 離心率為
. 平面上的動點
為橢圓
外一點,且過
點
引橢圓
的兩條切線互相垂直.
（1）求曲線
的方程；
（2）求動點
的軌跡方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】汽車是碳排放量比較大的交通工具,某地規定,從2017年開始,將對二氧化碳排放量超過130 g/km的輕型汽車進行懲罰性征稅,檢測單位對甲、乙兩品牌輕型汽車各抽取5輛進行二氧化碳排放量檢測,記錄如下(單位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | 100 | 160 |
經測算得乙品牌輕型汽車二氧化碳排放量的平均值為
=120 g/km.
(1)求表中x的值,并比較甲、乙兩品牌輕型汽車二氧化碳排放量的穩定性;
(2)從被檢測的5輛甲品牌輕型汽車中任取2輛,則至少有一輛二氧化碳排放量超過130 g/km的概率是多少?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
分別是橢圓
的左、右焦點，離心率為
， 
分別是橢圓的上、下頂點， 
.
(1)求橢圓
的方程；
(2)若直線
與橢圓
交于相異兩點
，且滿足直線
的斜率之積為
，證明：直線
恒過定點，并采定點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=Asin（ωx+φ）（A，ω，φ均為正的常數）的最小正周期為π，當x= 
時，函數f（x）取得最小值，則下列結論正確的是（ ）
A.f（2）＜f（﹣2）＜f（0）
B.f（0）＜f（2）＜f（﹣2）
C.f（﹣2）＜f（0）＜f（2）
D.f（2）＜f（0）＜f（﹣2）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
