
【題目】已知數列![]() 滿足:
滿足:![]() ,
,![]() ,其中
,其中![]() ,數列
,數列![]() 滿足:
滿足:![]()
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)證明:![]() 對任意
對任意![]() 均成立,并求數列
均成立,并求數列![]() 的通項公式;
的通項公式;
(3)是否存在正數![]() ,使得數列
,使得數列![]() 的每一項均為整數,如果不存在,說明理由,如果存在,求出所有的
的每一項均為整數,如果不存在,說明理由,如果存在,求出所有的![]() .
.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)證明見解析,
;(2)證明見解析,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據計算得到![]() ,
,![]() ,
,![]() ,再根據
,再根據![]() 與
與![]() 的關系,得到答案;(2)由條件可得
的關系,得到答案;(2)由條件可得![]() ,然后得到
,然后得到![]() ,兩式相減,從而進行證明,并以根據所證的式子可得到
,兩式相減,從而進行證明,并以根據所證的式子可得到![]() 的通項;(3)假設存在正數
的通項;(3)假設存在正數![]() ,由(2)可知
,由(2)可知 ,由
,由![]() ,得到
,得到![]() ,再利用數學歸納法進行證明
,再利用數學歸納法進行證明![]() 滿足題意.
滿足題意.
(1)![]() ,所以
,所以![]() ,
,
![]() 時
時![]() ,
,![]() 時
時![]()
![]() 時
時![]() ,
,
而![]()
所以![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)因為![]() ,
,
所以![]() ,
,
所以![]()
下式減上式,得![]() ,
,
整理得![]()
即有![]() ,
,
所以![]() ,
,
![]() ,
,
所以![]() ;
;
(3)假設存在正數![]() ,使得數列
,使得數列![]() 的每一項均為整數,
的每一項均為整數,
由(2)可知 ①,
①,
由![]() ,
,![]() ,可得
,可得![]() ,
,
當![]() 時,
時,![]() 為整數,利用
為整數,利用![]() ,
,
結合①式,反復遞推,可知![]() 每一項均為整數,所以符合題意,
每一項均為整數,所以符合題意,
當![]() 時,①式變為
時,①式變為 ②
②
下用數學歸納法證明![]() 為偶數,
為偶數,![]() 為整數
為整數
![]() 時,結論顯然成立,
時,結論顯然成立,
假設![]() 時,結論成立,此時
時,結論成立,此時![]() 為偶數,
為偶數,![]() 為整數,
為整數,
故![]() 時,
時,![]() 為偶數,
為偶數,![]() 為整數,
為整數,
所以![]() 時,命題也成立.
時,命題也成立.
所以數列![]() 為整數數列.此時
為整數數列.此時![]() 滿足題意.
滿足題意.
綜上所述,滿足題意的![]() 的取值集合為
的取值集合為![]() .
.


科目:高中數學 來源: 題型:
【題目】給出下列四個說法,其中正確的是( )
A.命題“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”
”
B.“![]() ”是“雙曲線
”是“雙曲線![]() 的離心率大于
的離心率大于![]() ”的充要條件
”的充要條件
C.命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命題“在![]() 中,若
中,若![]() ,則
,則![]() 是銳角三角形”的逆否命題是假命題
是銳角三角形”的逆否命題是假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校組織高考組考工作,為了搞好接待組委會招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,調查發現,男、女志愿者中分別有
名女志愿者,調查發現,男、女志愿者中分別有![]() 人和
人和![]() 人喜愛運動,其余不喜愛.
人喜愛運動,其余不喜愛.
(1)根據以上數據完成以下![]() 列聯表;并要求列聯表的獨立性檢驗,能否在犯錯誤的概率不超過
列聯表;并要求列聯表的獨立性檢驗,能否在犯錯誤的概率不超過![]() 的前提下認為性別與喜愛運動有關?
的前提下認為性別與喜愛運動有關?
喜愛運動 | 不喜愛運動 | 總計 | |
男 |
|
| |
女 |
|
| |
總計 |
|
(2)如果從喜歡運動的女志愿者中(其中恰有![]() 人會外語),抽取
人會外語),抽取![]() 名負責翻譯工作,則抽出的志愿者中
名負責翻譯工作,則抽出的志愿者中![]() 人恰有一人勝任翻譯工作的概率是多少?
人恰有一人勝任翻譯工作的概率是多少?
參考公式: ,其中
,其中![]() .
.
參考答數:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定橢圓![]() .稱圓心在原點O,半徑為
.稱圓心在原點O,半徑為![]() 的圓是橢圓C的“準圓”.若橢圓C的一個焦點為
的圓是橢圓C的“準圓”.若橢圓C的一個焦點為![]() ,其短軸上的一個端點到F的距離為
,其短軸上的一個端點到F的距離為![]() .
.
(1)求橢圓C的方程和其“準圓”方程;
(2)點P是橢圓C的“準圓”上的一個動點,過動點P作直線![]() ,使得
,使得![]() 與橢圓C都只有一個交點,試判斷
與橢圓C都只有一個交點,試判斷![]() 是否垂直?并說明理由.
是否垂直?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,設直線
,設直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,
兩點,![]() 為線段
為線段![]() 的中點.
的中點.

(1)若直線![]() 的傾斜角為
的傾斜角為![]() ,求
,求![]() 的值;
的值;
(2)設直線![]() 交直線
交直線![]() 于點
于點![]() ,證明:直線
,證明:直線![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() )以坐標原點為極點,
)以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 和
和![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比數列,求
成等比數列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在第十五次全國國民閱讀調查中,某地區調查組獲得一個容量為![]() 的樣本,其中城鎮居民
的樣本,其中城鎮居民![]() 人,農村居民
人,農村居民![]() 人.在這些居民中,經常閱讀的城鎮居民
人.在這些居民中,經常閱讀的城鎮居民![]() 人,農村居民
人,農村居民![]() 人.
人.
(1)填寫下面列聯表,并判斷是否有![]() 的把握認為,經常閱讀與居民居住地有關?
的把握認為,經常閱讀與居民居住地有關?
城鎮居民 | 農村居民 | 合計 | |
經常閱讀 |
|
| |
不經常閱讀 | |||
合計 |
|
(2)調查組從該樣本的城鎮居民中按分層抽樣抽取出![]() 人,參加一次閱讀交流活動,若活動主辦方從這
人,參加一次閱讀交流活動,若活動主辦方從這![]() 位居民中隨機選取
位居民中隨機選取![]() 人作交流發言,求被選中的
人作交流發言,求被選中的![]() 位居民都是經常閱讀居民的概率.
位居民都是經常閱讀居民的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高中年級開設了豐富多彩的校本課程,甲、乙兩班各隨機抽取了5名學生的學分,用莖葉圖表示.![]() ,
,![]() 分別表示甲、乙兩班各自5名學生學分的標準差,則
分別表示甲、乙兩班各自5名學生學分的標準差,則![]() _______
_______![]() .(填“
.(填“![]() ”“<”或“=”)
”“<”或“=”)
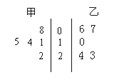
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com