
【題目】在平面直角坐標系![]() 中,動圓
中,動圓![]() 與圓
與圓![]() 外切,與圓
外切,與圓![]() 內切.
內切.
(1)求動圓圓心![]() 的軌跡方程;
的軌跡方程;
(2)直線![]() 過點
過點![]() 且與動圓圓心
且與動圓圓心![]() 的軌跡交于
的軌跡交于![]() 、
、![]() 兩點.是否存在
兩點.是否存在![]() 面積的最大值,若存在,求出
面積的最大值,若存在,求出![]() 的面積;若不存在,說明理由.
的面積;若不存在,說明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 面積的最大值為
面積的最大值為![]() ,理由見解析.
,理由見解析.
【解析】
(1)設動圓![]() 的半徑為
的半徑為![]() ,利用幾何關系轉化兩圓內切和外切的問題,可得出
,利用幾何關系轉化兩圓內切和外切的問題,可得出![]() ,可得知點
,可得知點![]() 的軌跡是以點
的軌跡是以點![]() 、
、![]() 為焦點的橢圓,并設該橢圓的方程為
為焦點的橢圓,并設該橢圓的方程為![]() ,利用橢圓的定義求出
,利用橢圓的定義求出![]() 的值,可求出
的值,可求出![]() 的值,由此可得出動點
的值,由此可得出動點![]() 的軌跡方程;
的軌跡方程;
(2)設直線![]() 的方程為
的方程為![]() ,設點
,設點![]() 、
、![]() ,將直線
,將直線![]() 的方程與橢圓的方程聯立,列出韋達定理,并計算出
的方程與橢圓的方程聯立,列出韋達定理,并計算出![]() 的面積關于
的面積關于![]() 的表達式,換元
的表達式,換元![]() ,利用雙勾函數的單調性可得出
,利用雙勾函數的單調性可得出![]() 面積的最大值.
面積的最大值.
(1)設點![]() ,動圓
,動圓![]() 的半徑為
的半徑為![]() ,
,
由題意知,![]() ,
,![]() ,
,![]()
由橢圓定義可知,動圓圓心![]() 在以
在以![]() 、
、![]() 為焦點的橢圓上,
為焦點的橢圓上,
設該橢圓的方程為![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
由于圓![]() 內切于圓
內切于圓![]() 于點
于點![]() ,則
,則![]() .
.
因此,動圓圓心![]() 的軌跡方程為
的軌跡方程為![]() ;
;
(2)存在![]() 面積的最大值.
面積的最大值.
因為直線![]() 過點
過點![]() ,可設直線
,可設直線![]() 的方程為
的方程為![]() 或
或![]() (舍).
(舍).
則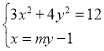 ,整理得
,整理得 ![]() .
.
由![]() .
.
設點![]() 、
、![]() ,則
,則![]() ,
,![]() .
.
則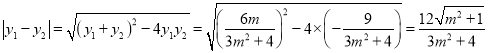 ,
,
因為![]() .
.
設![]() ,則
,則![]() ,則
,則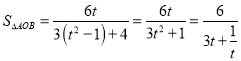 .
.
設![]() 在區間
在區間![]() 上為增函數,所以
上為增函數,所以![]() .
.
所以![]() ,當且僅當
,當且僅當![]() 時取等號,即
時取等號,即![]() .
.
因此,![]() 面積的最大值為
面積的最大值為![]() .
.


 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源: 題型:
【題目】如今我們的互聯網生活日益豐富,除了可以很方便地網購,網絡外賣也開始成為不少人日常生活中不可或缺的一部分![]() 市某調查機構針對該市市場占有率最高的兩種網絡外賣企業
市某調查機構針對該市市場占有率最高的兩種網絡外賣企業![]() 以下簡稱外賣A、外賣
以下簡稱外賣A、外賣![]() 的服務質量進行了調查,從使用過這兩種外賣服務的市民中隨機抽取了1000人,每人分別對這兩家外賣企業評分,滿分均為100分,并將分數分成5組,得到以下頻數分布表:
的服務質量進行了調查,從使用過這兩種外賣服務的市民中隨機抽取了1000人,每人分別對這兩家外賣企業評分,滿分均為100分,并將分數分成5組,得到以下頻數分布表:
分數 人數 種類 |
|
|
|
|
|
外賣A | 50 | 150 | 100 | 400 | 300 |
外賣B | 100 | 100 | 300 | 200 | 300 |
表中得分越高,說明市民對網絡外賣服務越滿意![]() 若得分不低于60分,則表明該市民對網絡外賣服務質量評價較高
若得分不低于60分,則表明該市民對網絡外賣服務質量評價較高![]() 現將分數按“服務質量指標”劃分成以下四個檔次:
現將分數按“服務質量指標”劃分成以下四個檔次:
分數 |
|
|
|
|
服務質量指標 | 0 | 1 | 2 | 3 |
視頻率為概率,解決下列問題:
![]() 從該市使用過外賣A的市民中任選5人,記對外賣A服務質量評價較高的人數為X,求X的數學期望.
從該市使用過外賣A的市民中任選5人,記對外賣A服務質量評價較高的人數為X,求X的數學期望.
![]() 從參與調查的市民中隨機抽取1人,試求其評分中外賣A的“服務質量指標”與外賣B的“服務質量指標”的差的絕對值等于2的概率;
從參與調查的市民中隨機抽取1人,試求其評分中外賣A的“服務質量指標”與外賣B的“服務質量指標”的差的絕對值等于2的概率;
![]() 在M市工作的小王決定從外賣A、外賣B這兩種網絡外賣中選擇一種長期使用,如果從這兩種外賣的“服務質量指標”的期望角度看,他選擇哪種外賣更合適?試說明理由.
在M市工作的小王決定從外賣A、外賣B這兩種網絡外賣中選擇一種長期使用,如果從這兩種外賣的“服務質量指標”的期望角度看,他選擇哪種外賣更合適?試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四面體ABCD中,平面DAC⊥底面ABC,![]() ,AD=CD=
,AD=CD=![]() ,O是AC的中點,E是BD的中點.
,O是AC的中點,E是BD的中點.
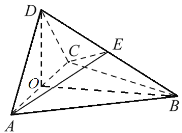
(1)證明:DO⊥底面ABC;
(2)求二面角D-AE-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是由非負整數組成的無窮數列,對每一個正整數
是由非負整數組成的無窮數列,對每一個正整數![]() ,該數列前
,該數列前![]() 項的最大值記為
項的最大值記為![]() ,第
,第![]() 項之后各項
項之后各項![]() 的最小值記為
的最小值記為![]() ,記
,記![]() .
.
(1)若數列![]() 的通項公式為
的通項公式為![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)證明:“數列![]() 單調遞增”是“
單調遞增”是“![]() ”的充要條件;
”的充要條件;
(3)若![]() 對任意
對任意![]() 恒成立,證明:數列
恒成立,證明:數列![]() 的通項公式為
的通項公式為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 上一點,經過點
上一點,經過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 、
、![]() 兩點(不同于點
兩點(不同于點![]() ),直線
),直線![]() 、
、![]() 分別交直線
分別交直線![]() 于點
于點![]() 、
、![]() .
.
(1)求拋物線方程及其焦點坐標;
(2)求證:以![]() 為直徑的圓恰好經過原點.
為直徑的圓恰好經過原點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以橢圓![]() :
:![]() 的中心
的中心![]() 為圓心,
為圓心,![]() 為半徑的圓稱為該橢圓的“準圓”,設橢圓
為半徑的圓稱為該橢圓的“準圓”,設橢圓![]() 的左頂點為
的左頂點為![]() ,左焦點為
,左焦點為![]() ,上頂點為
,上頂點為![]() ,且滿足
,且滿足![]() ,
,![]() .
.
(1)求橢圓![]() 及其“準圓"的方程;
及其“準圓"的方程;
(2)若過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,當
兩點,當![]() 時,試求直線
時,試求直線![]() 交“準圓”所得的弦長;
交“準圓”所得的弦長;
(3)射線![]() 與橢圓
與橢圓![]() 的“準圓”交于點
的“準圓”交于點![]() ,若過點
,若過點![]() 的直線
的直線![]() ,
,![]() 與橢圓
與橢圓![]() 都只有一個公共點,且與橢圓
都只有一個公共點,且與橢圓![]() 的“準圓”分別交于
的“準圓”分別交于![]() ,
,![]() 兩點,試問弦
兩點,試問弦![]() 是否為”準圓”的直徑?若是,請給出證明:若不是,請說明理由.
是否為”準圓”的直徑?若是,請給出證明:若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com