
【題目】已知曲線![]() 的方程為
的方程為![]() .
.
(1)當(dāng)![]() 時(shí),試確定曲線
時(shí),試確定曲線![]() 的形狀及其焦點(diǎn)坐標(biāo);
的形狀及其焦點(diǎn)坐標(biāo);
(2)若直線![]() 交曲線
交曲線![]() 于點(diǎn)
于點(diǎn)![]() 、
、![]() ,線段
,線段![]() 中點(diǎn)的橫坐標(biāo)為
中點(diǎn)的橫坐標(biāo)為![]() ,試問(wèn)此時(shí)曲線
,試問(wèn)此時(shí)曲線![]() 上是否存在不同的兩點(diǎn)
上是否存在不同的兩點(diǎn)![]() 、
、![]() 關(guān)于直線
關(guān)于直線![]() 對(duì)稱?
對(duì)稱?
(3)當(dāng)![]() 為大于1的常數(shù)時(shí),設(shè)
為大于1的常數(shù)時(shí),設(shè)![]() 是曲線
是曲線![]() 上的一點(diǎn),過(guò)點(diǎn)
上的一點(diǎn),過(guò)點(diǎn)![]() 作一條斜率為
作一條斜率為![]() 的直線
的直線![]() ,又設(shè)
,又設(shè)![]() 為原點(diǎn)到直線
為原點(diǎn)到直線![]() 的距離,
的距離,![]() 分別為點(diǎn)
分別為點(diǎn)![]() 與曲線
與曲線![]() 兩焦點(diǎn)的距離,求證
兩焦點(diǎn)的距離,求證![]() 是一個(gè)定值,并求出該定值.
是一個(gè)定值,并求出該定值.
【答案】(1) 曲線![]() 是焦點(diǎn)在
是焦點(diǎn)在![]() 軸上的橢圓,焦點(diǎn)坐標(biāo)為
軸上的橢圓,焦點(diǎn)坐標(biāo)為![]() ; (2) 見(jiàn)解析;(3)見(jiàn)證明
; (2) 見(jiàn)解析;(3)見(jiàn)證明
【解析】
(1)將a代入,兩邊平方并化簡(jiǎn),可得曲線C的方程及形狀;
(2)將![]() 代入曲線,利用PQ中點(diǎn)的橫坐標(biāo)為
代入曲線,利用PQ中點(diǎn)的橫坐標(biāo)為![]() ,求出m,驗(yàn)證判別式是否成立,可得結(jié)論.
,求出m,驗(yàn)證判別式是否成立,可得結(jié)論.
(3)將曲線C化簡(jiǎn),得到焦點(diǎn)坐標(biāo),求得![]() ,再求得點(diǎn)到直線
,再求得點(diǎn)到直線![]() 的距離,代入
的距離,代入![]() 化簡(jiǎn)得到定值.
化簡(jiǎn)得到定值.
(1)當(dāng)![]() 時(shí),
時(shí),![]() ,兩邊平方并化簡(jiǎn)得
,兩邊平方并化簡(jiǎn)得![]() ,
,
∴曲線![]() 是焦點(diǎn)在
是焦點(diǎn)在![]() 軸上的橢圓,其長(zhǎng)半軸長(zhǎng)為1,短半軸長(zhǎng)為
軸上的橢圓,其長(zhǎng)半軸長(zhǎng)為1,短半軸長(zhǎng)為![]() ,焦點(diǎn)坐標(biāo)為
,焦點(diǎn)坐標(biāo)為![]() ;
;
(2)將![]() 代入
代入![]() ,消去
,消去![]() ,
,
得![]() ,由題意,
,由題意,![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍),此時(shí),
(舍),此時(shí),![]() ,
,![]() ,
,
設(shè)![]() ,
,![]() ,
,![]() ,
,
將![]() 代入
代入![]() ,得
,得![]() ,則
,則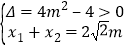 ,
,
![]() 的中點(diǎn)坐標(biāo)為
的中點(diǎn)坐標(biāo)為![]() 在對(duì)稱軸
在對(duì)稱軸![]() 上,∴
上,∴![]() ,解得
,解得![]() ,
,
不滿足![]() ,∴曲線
,∴曲線![]() 上不存在不同的兩點(diǎn)
上不存在不同的兩點(diǎn)![]() 、
、![]() 關(guān)于直線
關(guān)于直線![]() 對(duì)稱;
對(duì)稱;
(3)![]() ,兩焦點(diǎn)坐標(biāo)為
,兩焦點(diǎn)坐標(biāo)為![]() 、
、![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
∴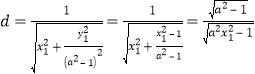 ,
,
用![]() 替換
替換![]() 中的
中的![]() ,
,
可得![]() ,∴
,∴![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】有下列四個(gè)命題:
(1)“若![]() ,則
,則![]() ,
,![]() 互為倒數(shù)”的逆命題;
互為倒數(shù)”的逆命題;
(2)“面積相等的三角形全等”的否命題;
(3)“若![]() ,則
,則![]() 無(wú)實(shí)數(shù)解”的否命題;
無(wú)實(shí)數(shù)解”的否命題;
(4)命題:“空間中到一個(gè)正四面體的六條棱所在的直線距離均相等的點(diǎn)有且只有![]() 個(gè)”; 其中真命題( )
個(gè)”; 其中真命題( )
A.(1)(2)B.(2)(3)C.(1)(2)(3)D.(1)(2)(4)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】有下列說(shuō)法:
①一支田徑隊(duì)有男女運(yùn)動(dòng)員98人,其中男運(yùn)動(dòng)員有56人.按男、女比例用分層抽樣的方法,從全體運(yùn)動(dòng)員中抽出一個(gè)容量為28的樣本,那么應(yīng)抽取女運(yùn)動(dòng)員人數(shù)是12人;
②在某項(xiàng)測(cè)量中,測(cè)量結(jié)果X服從正態(tài)分布N(1,σ2)(σ>0),若X在(0,1)內(nèi)取值的概率為0.4,則X在(0,2)內(nèi)取值的概率為0.8.
③廢品率x%和每噸生鐵成本y(元)之間的回歸直線方程為![]() 2x+256,這表明廢品率每增加1%,生鐵成本大約增加258元;
2x+256,這表明廢品率每增加1%,生鐵成本大約增加258元;
④為了檢驗(yàn)?zāi)撤N血清預(yù)防感冒的作用,把500名未使用血清和使用血清的人一年中的感冒記錄作比較,提出假設(shè)H0:“這種血清不能起到預(yù)防作用”,利用2×2列聯(lián)表計(jì)算得K2的觀測(cè)值k≈3.918,經(jīng)查對(duì)臨界值表知P(K2≥3841)≈0.05,由此,得出以下判斷:在犯錯(cuò)誤的概率不超過(guò)0.05的前提下認(rèn)為“這種血清能起到預(yù)防的作用”,
正確的有( )
A.①②④B.①②③C.①③D.③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知正方形![]() 的邊長(zhǎng)為2,
的邊長(zhǎng)為2, ![]() 是
是![]() 的中點(diǎn),以點(diǎn)
的中點(diǎn),以點(diǎn)![]() 為圓心,
為圓心, ![]() 長(zhǎng)為半徑作圓,點(diǎn)
長(zhǎng)為半徑作圓,點(diǎn)![]() 是該圓上的任一點(diǎn),則
是該圓上的任一點(diǎn),則![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)任意![]() ,函數(shù)
,函數(shù)![]() 滿足:
滿足:![]() ,
,![]() ,數(shù)列
,數(shù)列![]() 的前15項(xiàng)和為
的前15項(xiàng)和為![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() ,若數(shù)列
,若數(shù)列![]() 的前
的前![]() 項(xiàng)和的極限存在,則
項(xiàng)和的極限存在,則![]() ________.
________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司生產(chǎn)某種產(chǎn)品,一條流水線年產(chǎn)量為![]() 件,該生產(chǎn)線分為兩段,流水線第一段生產(chǎn)的半成品的質(zhì)量指標(biāo)會(huì)影響第二段生產(chǎn)成品的等級(jí),具體見(jiàn)下表:
件,該生產(chǎn)線分為兩段,流水線第一段生產(chǎn)的半成品的質(zhì)量指標(biāo)會(huì)影響第二段生產(chǎn)成品的等級(jí),具體見(jiàn)下表:
第一段生產(chǎn)的半成品質(zhì)量指標(biāo) |
|
|
|
第二段生產(chǎn)的成品為一等品概率 | 0.2 | 0.4 | 0.6 |
第二段生產(chǎn)的成品為二等品概率 | 0.3 | 0.3 | 0.3 |
第二段生產(chǎn)的成品為三等品概率 | 0.5 | 0.3 | 0.1 |
從第一道生產(chǎn)工序抽樣調(diào)查了![]() 件,得到頻率分布直方圖如圖:
件,得到頻率分布直方圖如圖:

若生產(chǎn)一件一等品、二等品、三等品的利潤(rùn)分別是![]() 元、
元、![]() 元、
元、![]() 元.
元.
(Ⅰ)以各組的中間值估計(jì)為該組半成品的質(zhì)量指標(biāo),估算流水線第一段生產(chǎn)的半成品質(zhì)量指標(biāo)的平均值;
(Ⅱ)將頻率估計(jì)為概率,試估算一條流水線一年能為該公司創(chuàng)造的利潤(rùn);
(Ⅲ)現(xiàn)在市面上有一種設(shè)備可以安裝到流水線第一段,價(jià)格是![]() 萬(wàn)元,使用壽命是
萬(wàn)元,使用壽命是![]() 年,安裝這種設(shè)備后,流水線第一段半成品的質(zhì)量指標(biāo)服從正態(tài)分布
年,安裝這種設(shè)備后,流水線第一段半成品的質(zhì)量指標(biāo)服從正態(tài)分布![]() ,且不影響產(chǎn)量.請(qǐng)你幫該公司作出決策,是否要購(gòu)買(mǎi)該設(shè)備?說(shuō)明理由.
,且不影響產(chǎn)量.請(qǐng)你幫該公司作出決策,是否要購(gòu)買(mǎi)該設(shè)備?說(shuō)明理由.
(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下表是![]() 年
年![]() 個(gè)重點(diǎn)城市(序號(hào)
個(gè)重點(diǎn)城市(序號(hào)![]() 為一線城市,其它為非一線城市)的月平均收入與房?jī)r(jià)對(duì)照表,根據(jù)表中數(shù)據(jù)并適當(dāng)修正,得到房?jī)r(jià)中位數(shù)與月平均收入的線性回歸方程是
為一線城市,其它為非一線城市)的月平均收入與房?jī)r(jià)對(duì)照表,根據(jù)表中數(shù)據(jù)并適當(dāng)修正,得到房?jī)r(jià)中位數(shù)與月平均收入的線性回歸方程是![]() ,我們把根據(jù)房?jī)r(jià)與月平均收入的線性回歸方程得到的房?jī)r(jià)稱為參考房?jī)r(jià),若實(shí)際房?jī)r(jià)中位數(shù)大于參考房?jī)r(jià),我們稱這個(gè)城市是“房?jī)r(jià)偏貴城市”.
,我們把根據(jù)房?jī)r(jià)與月平均收入的線性回歸方程得到的房?jī)r(jià)稱為參考房?jī)r(jià),若實(shí)際房?jī)r(jià)中位數(shù)大于參考房?jī)r(jià),我們稱這個(gè)城市是“房?jī)r(jià)偏貴城市”.
序號(hào) | 月評(píng)價(jià)收入 | 房?jī)r(jià)中位數(shù) | 參考房?jī)r(jià) | 序號(hào) | 月評(píng)價(jià)收入 | 房?jī)r(jià)中位數(shù) | 參考房?jī)r(jià) | 序號(hào) | 月評(píng)價(jià)收入 | 房?jī)r(jià)中位數(shù) | 參考房?jī)r(jià) |
1 | 10670 | 67822 | 11 | 7081 | 17327 | 25704 | 21 | 7081 | 14792 | 15972 | |
2 | 10015 | 52584 | 51180 | 12 | 7065 | 13918 | 19476 | 22 | 7065 | 18741 | 15780 |
3 | 9561 | 50900 | 45732 | 13 | 7027 | 16286 | 19404 | 23 | 7027 | 10538 | 15324 |
4 | 8798 | 30729 | 36576 | 14 | 6974 | 16667 | 18204 | 24 | 6974 | 12069 | 14688 |
5 | 7424 | 10926 | 20088 | 15 | 6920 | 9743 | 17760 | 25 | 6920 | 2333 | 14040 |
6 | 7825 | 26714 | 24900 | 16 | 6903 | 10627 | 18120 | 26 | 6903 | 13582 | 13836 |
7 | 7770 | 39723 | 24240 | 17 | 6884 | 29000 | 17388 | 27 | 6884 | 22126 | 13608 |
8 | 7750 | 15114 | 24000 | 18 | 6654 | 7979 | 16584 | 28 | 6654 | 12207 | 10848 |
9 | 7723 | 17727 | 23676 | 19 | 6648 | 12500 | 16920 | 29 | 6648 | 12472 | 10776 |
10 | 7635 | 13012 | 22620 | 20 | 6608 | 12298 | 16200 | 30 | 6608 | 16406 | 10286 |
(1)計(jì)算城市![]() 的參考房?jī)r(jià);
的參考房?jī)r(jià);
(2)從![]() 個(gè)一線城市中隨機(jī)選取
個(gè)一線城市中隨機(jī)選取![]() 個(gè)城市進(jìn)行調(diào)研,求恰好選到一個(gè)“房?jī)r(jià)偏貴城市”的概率;
個(gè)城市進(jìn)行調(diào)研,求恰好選到一個(gè)“房?jī)r(jià)偏貴城市”的概率;
(3)完成下面的![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 的把握認(rèn)為一線城市與該城市為“房?jī)r(jià)偏貴城市”有關(guān)?
的把握認(rèn)為一線城市與該城市為“房?jī)r(jià)偏貴城市”有關(guān)?
一般城市 | 非一線城市 | 總計(jì) | |
房?jī)r(jià)偏貴城市 | |||
不是房?jī)r(jià)偏貴城市 | |||
總計(jì) |
附參考公式及數(shù)據(jù):![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
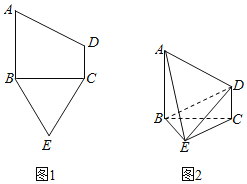
【題目】已知五邊形ABECD有一個(gè)直角梯形ABCD與一個(gè)等邊三角形BCE構(gòu)成,如圖1所示,![]() ,且
,且![]() ,將梯形ABCD沿著BC折起,形成如圖2所示的幾何體,且
,將梯形ABCD沿著BC折起,形成如圖2所示的幾何體,且![]() 平面BEC.
平面BEC.
![]() 求證:平面
求證:平面![]() 平面ADE;
平面ADE;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=1,AC=CD=DA=2,動(dòng)點(diǎn)M在邊DC上(不同于D點(diǎn)),P為邊AB上任意一點(diǎn),沿AM將△ADM翻折成△AD'M,當(dāng)平面AD'M垂直于平面ABC時(shí),線段PD'長(zhǎng)度的最小值為_____.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com