
【題目】下列關于古典概型的說法中正確的是( )
①試驗中所有可能出現的基本事件只有有限個;
②每個事件出現的可能性相等;
③每個基本事件出現的可能性相等;
④基本事件的總數為n,隨機事件A若包含k個基本事件,則![]() .
.
A. ②④ B. ③④ C. ①④ D. ①③④
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
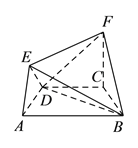
(![]() )求證:
)求證: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在線段
)在線段![]() (含端點)上,是否存在一點
(含端點)上,是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(![]() )見解析;(
)見解析;(![]() )
)![]() ;(
;(![]() )存在,
)存在, ![]()
【解析】試題分析:(1)由題意,證明![]() ,
, ![]() ,證明
,證明![]() 面
面![]() ;(2)建立空間直角坐標系,求平面
;(2)建立空間直角坐標系,求平面![]() 和平面
和平面![]() 的法向量,解得余弦值為
的法向量,解得余弦值為![]() ;(3)得
;(3)得![]() ,
, 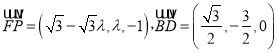 ,所以
,所以![]() ,
, ![]() ,所以存在
,所以存在![]() 為
為![]() 中點.
中點.
試題解析:
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() .
.
∵![]() ,且
,且![]() ,
,
![]() 、
、![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(![]() )知
)知![]() ,∴
,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標原點,
為坐標原點,
以![]() ,
, ![]() ,
, ![]() 為
為![]() ,
, ![]() ,
, ![]() 軸建系.
軸建系.
設![]() ,則
,則![]() ,
, ![]() ,
,  ,
, ![]() ,
, ![]() ,
,
∴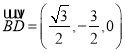 ,
, ![]() .
.
設![]() 的一個法向量為
的一個法向量為![]() ,
,
∴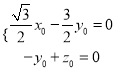 ,取
,取![]() ,則
,則![]() .
.
由于![]() 是面
是面![]() 的法向量,
的法向量,
則 .
.
∵二面角![]() 為銳二面角,∴余弦值為
為銳二面角,∴余弦值為![]() .
.
(![]() )存在點
)存在點![]() .
.
設![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 面
面![]() ,
, 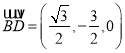 .
.
若![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴存在
,∴存在![]() 為
為![]() 中點.
中點.

【題型】解答題
【結束】
19
【題目】已知函數![]() .
.
(![]() )當
)當![]() 時,求此函數對應的曲線在
時,求此函數對應的曲線在![]() 處的切線方程.
處的切線方程.
(![]() )求函數
)求函數![]() 的單調區間.
的單調區間.
(![]() )對
)對![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 經過點
經過點![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過坐標原點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,過點
兩點,過點![]() 作
作![]() 的平行線交橢圓
的平行線交橢圓![]() 于
于![]() 、
、![]() 兩點.是否存在常數
兩點.是否存在常數![]() , 滿足
, 滿足![]() ?若存在,求出這個常數;若不存在,請說明理由.
?若存在,求出這個常數;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 為偶函數,且當
為偶函數,且當![]() 時,
時,![]() .記
.記![]() .給出下列關于函數
.給出下列關于函數![]() 的說法:①當
的說法:①當![]() 時,
時,![]() ;②函數
;②函數![]() 為奇函數;③函數
為奇函數;③函數![]() 在
在![]() 上為增函數;④函數
上為增函數;④函數![]() 的最小值為
的最小值為![]() ,無最大值.其中正確的是______.
,無最大值.其中正確的是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,且函數
,且函數![]() 是偶函數.
是偶函數.
(1)求![]() 的解析式;.
的解析式;.
(2)若不等式![]() 在
在![]() 上恒成立,求n的取值范圍;
上恒成立,求n的取值范圍;
(3)若函數 恰好有三個零點,求k的值及該函數的零點.
恰好有三個零點,求k的值及該函數的零點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.過![]() ,
,![]() 兩點的直線方程為
兩點的直線方程為![]()
B.點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]()
C.直線![]() 與兩坐標軸圍成的三角形的面積是2
與兩坐標軸圍成的三角形的面積是2
D.經過點![]() 且在
且在![]() 軸和
軸和![]() 軸上截距都相等的直線方程為
軸上截距都相等的直線方程為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的一條直角是橢圓
的一條直角是橢圓![]() 的長軸,動直線
的長軸,動直線![]() ,當
,當![]() 過橢圓
過橢圓![]() 上一點
上一點![]() 且與圓
且與圓![]() 相交于點
相交于點![]() 時,弦
時,弦![]() 的最小值為
的最小值為![]() .
.
(1)求圓即橢圓![]() 的方程;
的方程;
(2)若直線![]() 是橢圓
是橢圓![]() 的一條切線,
的一條切線,![]() 是切線上兩個點,其橫坐標分別為
是切線上兩個點,其橫坐標分別為![]() ,那么以
,那么以![]() 為直徑的圓是否經過
為直徑的圓是否經過![]() 軸上的定點?如果存在,求出定點坐標;若不存在,請說明理由.
軸上的定點?如果存在,求出定點坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在發生某公共衛生事件期間,有專業機構認為該事件在一段時間沒有發生在規模群體感染的標志為“連續10天,每天新增疑似病例不超過7人”.根據過去10天甲、乙、丙、丁四地新增疑似病例數據,一定符合該標志的是
A. 甲地:總體均值為3,中位數為4 B. 乙地:總體均值為1,總體方差大于0
C. 丙地:中位數為2,眾數為3 D. 丁地:總體均值為2,總體方差為3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com