【題目】已知函數(shù)
，
．
（1）討論
的單調(diào)性；
（2）若有兩個極值點
，求
的最大值．
【答案】（1）分類討論，詳見解析；（2）
.
【解析】
（1）求出導(dǎo)函數(shù)，根據(jù)二次函數(shù)的
與
的關(guān)系來分類討論函數(shù)的單調(diào)性，并注意一元二次方程根的正負與定義域的關(guān)系；
（2）由
是兩個極值點得到對應(yīng)的韋達定理形式，然后利用條件將
轉(zhuǎn)變?yōu)殛P(guān)于某一變量的新函數(shù)，分析新函數(shù)的單調(diào)性從而確定出新函數(shù)的最大值即的最大值.
（1）
，
，
，
當(dāng)
，即
時，
，此時
在
上單調(diào)遞增；
當(dāng)
時，
有兩個負根，此時在上單調(diào)遞增；
當(dāng)
時，有兩個正根，分別為
，
，
此時在
，
上單調(diào)遞增，在
上單調(diào)遞減．
綜上可得:
時，在上單調(diào)遞增，
時，在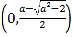
，
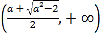上單調(diào)遞增，在
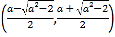上單調(diào)遞減．
（2）由（1）可得
，，
，
，
∵，
，∴
，
，
∴
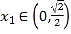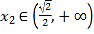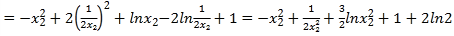
令
，則
當(dāng)
時，
；當(dāng)
時，
∴
在
上單調(diào)遞增，在
單調(diào)遞減
∴
∴的最大值為．
金版課堂課時訓(xùn)練系列答案
單元全能練考卷系列答案
新黃岡兵法密卷系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】函數(shù)①
；②
；③
；④
；其中對于
定義域內(nèi)任意一個自變量
都存在唯一自變量
，使得
成立的函數(shù)是（）
A.①③B.②③C.①②④D.③
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若定義在
上，且不恒為零的函數(shù)
滿足：對于任意實數(shù)
和
，總有
恒成立，則稱
為“類余弦型”函數(shù).
（1）已知為“類余弦型”函數(shù)，且
，求
和
的值；
（2）證明：函數(shù)為偶函數(shù)；
（3）若為“類余弦型”函數(shù)，且對于任意非零實數(shù)
，總有
，設(shè)有理數(shù)
、
滿足
，判斷
和
大小關(guān)系，并證明你的結(jié)論.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，四棱錐
的一個側(cè)面
為等邊三角形，且平面
平面
，四邊形是平行四邊形，
，
，
.
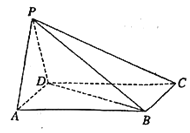
（1）求證：
；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】身體素質(zhì)拓展訓(xùn)練中，人從豎直墻壁的頂點A沿光滑桿自由下滑到傾斜的木板上（人可看作質(zhì)點），若木板的傾斜角不同，人沿著三條不同路徑AB、AC、AD滑到木板上的時間分別為t1、t2、t3，若已知AB、AC、AD與板的夾角分別為70o、90o和105o，則（ ）
A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能確定t1、t2、t3之間的關(guān)系
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
，函數(shù)
，且曲線
在
處的切線與直線
垂直.
（I）求函數(shù)
在區(qū)間
上的極大值；
（II）求證：當(dāng)
時，
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列四種說法中，錯誤的個數(shù)是（ ）
①命題“
，
”的否定是“
，
”；
②命題“
為真”是命題“
為真”的必要不充分條件；
③“若
，則
”的逆命題為真；
④若實數(shù)
，
，則滿足
的概率為
.
A.
個B.
個C.
個D.
個
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列命題中：
①若樣本數(shù)據(jù)
的方差為16，則數(shù)據(jù)
的方差為64；
②“平面向量
夾角為銳角，則
”的逆命題為真命題；
③命題“
，
”的否定是“
，
”；
④若：
，
，則
是
的充分不必要條件.
真命題的個數(shù)序號_________.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
為實數(shù))的圖像在點
處的切線方程為
.
（1）求實數(shù)
的值及函數(shù)
的單調(diào)區(qū)間；
（2）設(shè)函數(shù)
，證明
時， 
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com