
已知函數(shù) ,其中a>0.
,其中a>0.
(Ⅰ)求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若直線(xiàn) 是曲線(xiàn)
是曲線(xiàn) 的切線(xiàn),求實(shí)數(shù)a的值;
的切線(xiàn),求實(shí)數(shù)a的值;
(Ⅲ)設(shè) ,求
,求 在區(qū)間
在區(qū)間 上的最大值(其中e為自然對(duì)的底數(shù))。
上的最大值(其中e為自然對(duì)的底數(shù))。
(Ⅰ)函數(shù)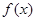 的單調(diào)遞增區(qū)間為(0,2),遞減區(qū)間為(-∞,0)和(2,+∞);(Ⅱ)
的單調(diào)遞增區(qū)間為(0,2),遞減區(qū)間為(-∞,0)和(2,+∞);(Ⅱ)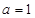 ;(Ⅲ)
;(Ⅲ)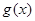 在區(qū)間
在區(qū)間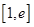 上的最大值為0.
上的最大值為0.
【解析】
試題分析:(Ⅰ)求函數(shù)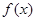 的單調(diào)區(qū)間,首先對(duì)函數(shù)
的單調(diào)區(qū)間,首先對(duì)函數(shù)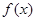 求導(dǎo),得函數(shù)
求導(dǎo),得函數(shù)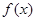 導(dǎo)函數(shù),直接讓導(dǎo)函數(shù)大于0,解出大于零的范圍,就求出增區(qū)間,令導(dǎo)函數(shù)小于0,解出小于零的范圍,從而求出減區(qū)間;(Ⅱ)直線(xiàn)
導(dǎo)函數(shù),直接讓導(dǎo)函數(shù)大于0,解出大于零的范圍,就求出增區(qū)間,令導(dǎo)函數(shù)小于0,解出小于零的范圍,從而求出減區(qū)間;(Ⅱ)直線(xiàn)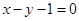 是曲線(xiàn)
是曲線(xiàn)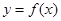 的切線(xiàn),由導(dǎo)數(shù)的幾何意義,利用切線(xiàn)的斜率即為切點(diǎn)處的導(dǎo)數(shù)值,以及切點(diǎn)即在直線(xiàn)上,又在曲線(xiàn)上,即為的共同點(diǎn),聯(lián)立方程組,解方程組,即可求實(shí)數(shù)
的切線(xiàn),由導(dǎo)數(shù)的幾何意義,利用切線(xiàn)的斜率即為切點(diǎn)處的導(dǎo)數(shù)值,以及切點(diǎn)即在直線(xiàn)上,又在曲線(xiàn)上,即為的共同點(diǎn),聯(lián)立方程組,解方程組,即可求實(shí)數(shù)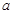 的值;(Ⅲ)求
的值;(Ⅲ)求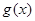 在區(qū)間
在區(qū)間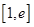 上的最大值,可利用導(dǎo)數(shù)來(lái)求,先求出
上的最大值,可利用導(dǎo)數(shù)來(lái)求,先求出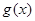 的解析式,由
的解析式,由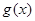 的解析式求出
的解析式求出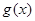 的導(dǎo)函數(shù),令
的導(dǎo)函數(shù),令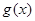 的導(dǎo)函數(shù)
的導(dǎo)函數(shù)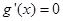 ,解出
,解出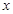 的值,從而確定最大值,由于含有參數(shù)
的值,從而確定最大值,由于含有參數(shù)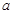 ,因此需分情況討論,從而求得其在區(qū)間
,因此需分情況討論,從而求得其在區(qū)間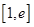 上的最大值.
上的最大值.
試題解析:(Ⅰ)①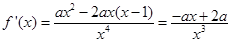 (
(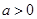 )
)
令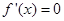 ,則
,則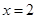 ,又
,又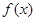 的定義域是
的定義域是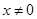

∴函數(shù)f(x)的單調(diào)遞增區(qū)間為(0,2),遞減區(qū)間為(-∞,0)和(2,+∞)(4分)
(II)設(shè)切點(diǎn)為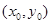 則
則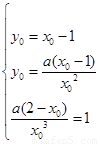 解得
解得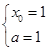 7分
7分
(III)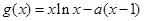
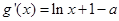
令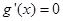 ,則
,則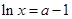 ,
,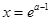
①當(dāng)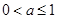 時(shí),
時(shí),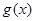 在
在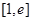 單調(diào)增加
單調(diào)增加 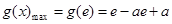 9分
9分
②當(dāng)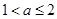 時(shí),
時(shí),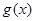 在
在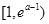 單調(diào)減少,在
單調(diào)減少,在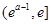 單調(diào)增加;
單調(diào)增加;
若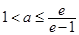 時(shí),
時(shí),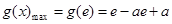 ;
;
若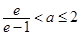 時(shí),
時(shí),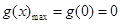 ; 11分
; 11分
③當(dāng)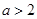 時(shí),
時(shí),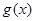 在
在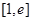 上單調(diào)遞減,
上單調(diào)遞減,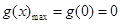 ;
;
綜上所述,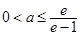 時(shí),
時(shí),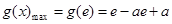 ;
;
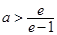 時(shí),
時(shí),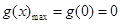 。 14分
。 14分
考點(diǎn):利用導(dǎo)數(shù)求閉區(qū)間上函數(shù)的最值;利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性.


 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
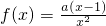 ,其中a>0.
,其中a>0.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
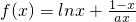 ,其中a為大于零的常數(shù).
,其中a為大于零的常數(shù).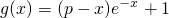 ,若存在x0∈[1,e],使不等式g(x0)≥lnx0成立,求實(shí)數(shù)p的取值范圍.(e為自然對(duì)數(shù)的底)
,若存在x0∈[1,e],使不等式g(x0)≥lnx0成立,求實(shí)數(shù)p的取值范圍.(e為自然對(duì)數(shù)的底)查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2012-2013學(xué)年山東省萊蕪市鳳城高中高三(上)第三次質(zhì)量檢測(cè)數(shù)學(xué)試卷(文科)(解析版) 題型:解答題
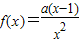 ,其中a>0.
,其中a>0.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010-2011學(xué)年四川省成都外國(guó)語(yǔ)學(xué)校高三(下)4月月考數(shù)學(xué)試卷(理科)(解析版) 題型:解答題
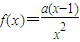 ,其中a>0.
,其中a>0.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年湖南省岳陽(yáng)市炎陵一中高三第六次月考數(shù)學(xué)試卷(文科)(解析版) 題型:解答題
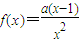 ,其中a>0.
,其中a>0.查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com