
【題目】一種擲骰子走跳棋的游戲:棋盤上標(biāo)有第0站、第1站、第2站、…、第100站,共101站,設(shè)棋子跳到第n站的概率為![]() ,一枚棋子開始在第0站,棋手每擲一次骰子,棋子向前跳動(dòng)一次.若擲出奇數(shù)點(diǎn),棋子向前跳一站;若擲出偶數(shù)點(diǎn),棋子向前跳兩站,直到棋子跳到第99站(獲勝)或第100站(失敗)時(shí),游戲結(jié)束(骰子是用一種均勻材料做成的立方體形狀的游戲玩具,它的六個(gè)面分別標(biāo)有點(diǎn)數(shù)1,2,3,4,5,6).
,一枚棋子開始在第0站,棋手每擲一次骰子,棋子向前跳動(dòng)一次.若擲出奇數(shù)點(diǎn),棋子向前跳一站;若擲出偶數(shù)點(diǎn),棋子向前跳兩站,直到棋子跳到第99站(獲勝)或第100站(失敗)時(shí),游戲結(jié)束(骰子是用一種均勻材料做成的立方體形狀的游戲玩具,它的六個(gè)面分別標(biāo)有點(diǎn)數(shù)1,2,3,4,5,6).
(1)求![]() ,
,![]() ,
,![]() ,并根據(jù)棋子跳到第n站的情況,試用
,并根據(jù)棋子跳到第n站的情況,試用![]() 和
和![]() 表示
表示![]() ;
;
(2)求證:![]() 為等比數(shù)列;
為等比數(shù)列;
(3)求玩該游戲獲勝的概率.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)證明見解析;(3)
;(2)證明見解析;(3)![]() .
.
【解析】
(1) 在第0站是必然事件,所以![]() .棋子跳到第1站,只有一種情形,第一次擲骰子出現(xiàn)奇數(shù)點(diǎn),可求出
.棋子跳到第1站,只有一種情形,第一次擲骰子出現(xiàn)奇數(shù)點(diǎn),可求出![]() ,棋子跳到第2站,包括兩種情形,①第一次擲骰子岀現(xiàn)偶數(shù)點(diǎn),②前兩次擲骰子出現(xiàn)奇數(shù)點(diǎn),可求出
,棋子跳到第2站,包括兩種情形,①第一次擲骰子岀現(xiàn)偶數(shù)點(diǎn),②前兩次擲骰子出現(xiàn)奇數(shù)點(diǎn),可求出![]() .棋子跳到第
.棋子跳到第![]() 站,包括兩種情形,①棋子先跳到第
站,包括兩種情形,①棋子先跳到第![]() 站,又?jǐn)S骰子出現(xiàn)偶數(shù)點(diǎn), ②棋子先跳到第
站,又?jǐn)S骰子出現(xiàn)偶數(shù)點(diǎn), ②棋子先跳到第![]() 站,又?jǐn)S骰子出現(xiàn)奇數(shù)點(diǎn),進(jìn)行求解.
站,又?jǐn)S骰子出現(xiàn)奇數(shù)點(diǎn),進(jìn)行求解.
(2) 由(1)知,![]() ,所以
,所以![]() 可證.
可證.
(3) 該游戲獲勝的概率,即求![]() ,由(2)用累加法可求解.
,由(2)用累加法可求解.
(1)棋子開始在第0站是必然事件,所以![]() .
.
棋子跳到第1站,只有一種情形,第一次擲骰子出現(xiàn)奇數(shù)點(diǎn),其概率為![]() ,所以
,所以![]() .
.
棋子跳到第2站,包括兩種情形,①第一次擲骰子岀現(xiàn)偶數(shù)點(diǎn),其概率為![]() ;②前兩次擲骰子出現(xiàn)奇數(shù)點(diǎn),其概率為
;②前兩次擲骰子出現(xiàn)奇數(shù)點(diǎn),其概率為![]() ,所以
,所以![]() .
.
棋子跳到第![]() 站,包括兩種情形,①棋子先跳到第
站,包括兩種情形,①棋子先跳到第![]() 站,又?jǐn)S骰子出現(xiàn)偶數(shù)點(diǎn),其概率為
站,又?jǐn)S骰子出現(xiàn)偶數(shù)點(diǎn),其概率為![]() ;②棋子先跳到第
;②棋子先跳到第![]() 站,又?jǐn)S骰子出現(xiàn)奇數(shù)點(diǎn),其概率為
站,又?jǐn)S骰子出現(xiàn)奇數(shù)點(diǎn),其概率為![]() .
.
故![]() .
.
(2)由(1)知,![]() ,所以
,所以![]() .
.
又因?yàn)?/span>![]() ,
,
所以![]() 是首項(xiàng)為
是首項(xiàng)為![]() ,公比為
,公比為![]() 的等比數(shù)列.
的等比數(shù)列.
(3)由(2)知,![]() .
.
所以![]()
![]()
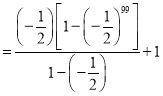
![]() .
.
所以玩該游戲獲勝的概率為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地有種特產(chǎn)水果很受當(dāng)?shù)乩习傩諝g迎,但該種水果只能在9月份銷售,且該種水果只能當(dāng)天食用口感最好,隔天食用口感較差。某超市每年9月份都銷售該特產(chǎn)水果,每天計(jì)劃進(jìn)貨量相同,進(jìn)貨成本每公斤8元,銷售價(jià)每公斤12元;當(dāng)天未賣出的水果則轉(zhuǎn)賣給水果罐頭廠,但每公斤只能賣到5元。根據(jù)往年銷售經(jīng)驗(yàn),每天需求量與當(dāng)?shù)貧鉁胤秶幸欢P(guān)系。如果氣溫不低于30度,需求量為5000公斤;如果氣溫位于![]() ,需求量為3500公斤;如果氣溫低于25度,需求量為2000公斤;為了制定今年9月份訂購(gòu)計(jì)劃,統(tǒng)計(jì)了前三年9月份的氣溫范圍數(shù)據(jù),得下面的頻數(shù)分布表
,需求量為3500公斤;如果氣溫低于25度,需求量為2000公斤;為了制定今年9月份訂購(gòu)計(jì)劃,統(tǒng)計(jì)了前三年9月份的氣溫范圍數(shù)據(jù),得下面的頻數(shù)分布表
氣溫范圍 |
|
|
|
|
|
天數(shù) | 4 | 14 | 36 | 21 | 15 |
以氣溫范圍位于各區(qū)間的頻率代替氣溫范圍位于該區(qū)間的概率.
(1)求今年9月份這種水果一天需求量![]() (單位:公斤)的分布列和數(shù)學(xué)期望;
(單位:公斤)的分布列和數(shù)學(xué)期望;
(2)設(shè)9月份一天銷售特產(chǎn)水果的利潤(rùn)為![]() (單位:元),當(dāng)9月份這種水果一天的進(jìn)貨量為
(單位:元),當(dāng)9月份這種水果一天的進(jìn)貨量為![]() (單位:公斤)為多少時(shí),
(單位:公斤)為多少時(shí),![]() 的數(shù)學(xué)期望達(dá)到最大值,最大值為多少?
的數(shù)學(xué)期望達(dá)到最大值,最大值為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在創(chuàng)建“全國(guó)文明城市”過(guò)程中,銀川市“創(chuàng)城辦”為了調(diào)查市民對(duì)創(chuàng)城工作的了解情況,進(jìn)行了一次創(chuàng)城知識(shí)問(wèn)卷調(diào)查(一位市民只能參加一次)通過(guò)隨機(jī)抽樣,得到參加問(wèn)卷調(diào)查的100人的得分統(tǒng)計(jì)結(jié)果如表所示:
組別 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
頻數(shù) | 2 | 13 | 21 | 25 | 24 | 11 | 4 |
(1)由頻數(shù)分布表可以大致認(rèn)為,此次問(wèn)卷調(diào)查的得分Z![]() N(μ,198),μ近似為這100人得分的平均值(同一組中的數(shù)據(jù)用該組區(qū)間的左端點(diǎn)值作代表),
N(μ,198),μ近似為這100人得分的平均值(同一組中的數(shù)據(jù)用該組區(qū)間的左端點(diǎn)值作代表),
①求μ的值;
②利用該正態(tài)分布,求![]() ;
;
(2)在(1)的條件下,“創(chuàng)城辦”為此次參加問(wèn)卷調(diào)查的市民制定如下獎(jiǎng)勵(lì)方案:
①得分不低于![]() 的可以獲贈(zèng)2次隨機(jī)話費(fèi),得分低于
的可以獲贈(zèng)2次隨機(jī)話費(fèi),得分低于![]() 的可以獲贈(zèng)1次隨機(jī)話費(fèi);
的可以獲贈(zèng)1次隨機(jī)話費(fèi);
②每次獲贈(zèng)的隨機(jī)話費(fèi)和對(duì)應(yīng)的概率為:
贈(zèng)送話費(fèi)的金額(單元:元) | 20 | 50 |
概率 |
|
|
現(xiàn)有市民甲參加此次問(wèn)卷調(diào)查,記![]() (單位:元)為該市民參加問(wèn)卷調(diào)查獲贈(zèng)的話費(fèi),求
(單位:元)為該市民參加問(wèn)卷調(diào)查獲贈(zèng)的話費(fèi),求![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
參考數(shù)據(jù)與公式:![]() .若
.若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】從拋物線![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() 向
向![]() 軸作垂線段垂足為
軸作垂線段垂足為![]() ,點(diǎn)
,點(diǎn)![]() 是線段
是線段![]() 上的一點(diǎn),且滿足
上的一點(diǎn),且滿足![]() .
.
(1)求點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設(shè)直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 為軌跡
為軌跡![]() 上異于
上異于![]() 的任意一點(diǎn),直線
的任意一點(diǎn),直線![]() 分別與直線
分別與直線![]() 交于
交于![]() 兩點(diǎn).問(wèn):
兩點(diǎn).問(wèn):![]() 軸正半軸上是否存在定點(diǎn)使得以
軸正半軸上是否存在定點(diǎn)使得以![]() 為直徑的圓過(guò)該定點(diǎn)?若存在,求出符合條件的定點(diǎn)坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
為直徑的圓過(guò)該定點(diǎn)?若存在,求出符合條件的定點(diǎn)坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是某市10月1日至14日的空氣質(zhì)量指數(shù)趨勢(shì)圖,空氣質(zhì)量指數(shù)越小表示空氣質(zhì)量越好,空氣質(zhì)量指數(shù)小于100表示空氣質(zhì)量?jī)?yōu)良,下列敘述中不正確的是( )

A.這14天中有7天空氣質(zhì)量?jī)?yōu)良
B.這14天中空氣質(zhì)量指數(shù)的中位數(shù)是103
C.從10月11日到10月14日,空氣質(zhì)量越來(lái)越好
D.連續(xù)三天中空氣質(zhì)量指數(shù)方差最大的是10月5日至10月7日
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐P-ABCD中,![]() 平面PCD,
平面PCD,![]() ,
,![]() ,
,![]() ,E為AD的中點(diǎn),AC與BE相交于點(diǎn)O.
,E為AD的中點(diǎn),AC與BE相交于點(diǎn)O.
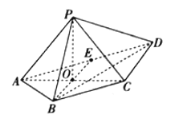
(1)證明:![]() 平面ABCD.
平面ABCD.
(2)求直線BC與平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某籃球隊(duì)甲、乙兩名運(yùn)動(dòng)員練習(xí)罰球,每人練習(xí)10組,每組罰球40個(gè).命中個(gè)數(shù)的莖葉圖如圖,則下面結(jié)論中錯(cuò)誤的一個(gè)是( )

A. 甲的極差是29 B. 甲的中位數(shù)是24
C. 甲罰球命中率比乙高 D. 乙的眾數(shù)是21
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】部分與整體以某種相似的方式呈現(xiàn)稱為分形.謝爾賓斯基三角形是一種分形,由波蘭數(shù)學(xué)家謝爾賓斯基1915年提出.具體操作是取一個(gè)實(shí)心三角形,沿三角形的三邊中點(diǎn)連線,將它分成4個(gè)小三角形,去掉中間的那一個(gè)小三角形后,對(duì)其余3個(gè)小三角形重復(fù)上述過(guò)程逐次得到各個(gè)圖形,如圖.

現(xiàn)在上述圖(3)中隨機(jī)選取一個(gè)點(diǎn),則此點(diǎn)取自陰影部分的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在寬為![]() 的路邊安裝路燈,燈柱
的路邊安裝路燈,燈柱![]() 高為
高為![]() ,燈桿
,燈桿![]() 是半徑為
是半徑為![]() 的圓
的圓![]() 的一段劣弧.路燈采用錐形燈罩,燈罩頂
的一段劣弧.路燈采用錐形燈罩,燈罩頂![]() 到路面的距離為
到路面的距離為![]() ,到燈柱所在直線的距離為
,到燈柱所在直線的距離為![]() .設(shè)
.設(shè)![]() 為燈罩軸線與路面的交點(diǎn),圓心
為燈罩軸線與路面的交點(diǎn),圓心![]() 在線段
在線段![]() 上.
上.

(1)當(dāng)![]() 為何值時(shí),點(diǎn)
為何值時(shí),點(diǎn)![]() 恰好在路面中線上?
恰好在路面中線上?
(2)記圓心![]() 在路面上的射影為
在路面上的射影為![]() ,且
,且![]() 在線段
在線段![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com