
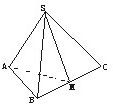
 如圖,正三棱錐S-ABC中,底面的邊長是3,棱錐的側面積等于底面積的2倍,M是BC的中點.
如圖,正三棱錐S-ABC中,底面的邊長是3,棱錐的側面積等于底面積的2倍,M是BC的中點.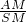 的值;
的值;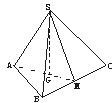 解:(1)∵SB=SC,AB=AC,M為BC的中點,
解:(1)∵SB=SC,AB=AC,M為BC的中點, BC×SM=2×
BC×SM=2× BC×AM,得
BC×AM,得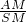 =
= .
. AM.
AM. AM=
AM= ×3GM=2GM,
×3GM=2GM, ,GM=
,GM= ,SG=GMtan60°=
,SG=GMtan60°= •
• =
= .
. S△ABC•SG=
S△ABC•SG= •
• •
• =
= .
.

科目:高中數學 來源: 題型:
 如圖,正三棱錐S-ABC中,側面SAB與底面ABC所成的二面角等于α,動點P在側面SAB內,PQ⊥底面ABC,垂足為Q,PQ=PS•sinα,則動點P的軌跡為( )
如圖,正三棱錐S-ABC中,側面SAB與底面ABC所成的二面角等于α,動點P在側面SAB內,PQ⊥底面ABC,垂足為Q,PQ=PS•sinα,則動點P的軌跡為( )| A、線段 | B、圓 | C、一段圓弧 | D、一段拋物線 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,正三棱錐S-ABC中,∠BSC=40°,SB=2,一質點自點B出發,沿著三棱錐的側面繞行一周回到點B的最短路線的長為( )
如圖,正三棱錐S-ABC中,∠BSC=40°,SB=2,一質點自點B出發,沿著三棱錐的側面繞行一周回到點B的最短路線的長為( )| A、2 | ||
| B、3 | ||
C、2
| ||
D、3
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,正三棱錐S-ABC中,底面的邊長是3,棱錐的側面積等于底面積的2倍,M是BC的中點.
如圖,正三棱錐S-ABC中,底面的邊長是3,棱錐的側面積等于底面積的2倍,M是BC的中點.| AM | SM |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com