
���}Ŀ����ֱ������(bi��o)ϵ![]() �У��A
�У��A![]() �ą���(sh��)����
�ą���(sh��)����![]() ��
��![]() �酢��(sh��)������
�酢��(sh��)������![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ��
�S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ��
��1����A![]() �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣�
��2��ֱ��![]() �ĘO����(bi��o)������
�ĘO����(bi��o)������![]() ���侀
���侀![]() �c�A
�c�A![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ��
��![]() ���cֱ��
���cֱ��![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ����
����![]() ���L(zh��ng)��
���L(zh��ng)��
���𰸡���1��![]() ����2��
����2��![]()
��������
��1�����ɈA�ą���(sh��)������ȥ����(sh��)���õ��A����ͨ���̣����ɘO����(bi��o)�cֱ������(bi��o)�Ļ�����ʽ�����ɵó��A�ĘO����(bi��o)���̣�
��2�����}�⣬���O(sh��)![]() ���c(di��n)�ĘO����(bi��o)�飺
���c(di��n)�ĘO����(bi��o)�飺![]() ��
��![]() ����
����![]() ����ֱ��
����ֱ��![]() �ĘO����(bi��o)���̣��õ�
�ĘO����(bi��o)���̣��õ�![]() ����
����![]() ����A�ĘO����(bi��o)���̣��õ�
����A�ĘO����(bi��o)���̣��õ�![]() ������
������![]() �����ɵó��Y(ji��)��.
�����ɵó��Y(ji��)��.
��1����?y��n)飬�A![]() �ą���(sh��)����
�ą���(sh��)����![]() ��
��![]() �酢��(sh��)������ȥ����(sh��)�ɵã�
�酢��(sh��)������ȥ����(sh��)�ɵã�![]() ��
��
��![]() ����
����![]() ������(ji��n)�ã�
������(ji��n)�ã�![]() ������ˈA�ĘO����(bi��o)���̣�
������ˈA�ĘO����(bi��o)���̣�
��2���O(sh��)![]() ���c(di��n)�ĘO����(bi��o)�飺
���c(di��n)�ĘO����(bi��o)�飺![]() ��
��![]() ��
��
��?y��n)�ֱ��![]() �ĘO����(bi��o)������
�ĘO����(bi��o)������![]() ���侀
���侀![]() ��
��
��![]() ����
����![]() ��
��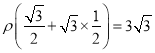 ����
����![]() ��
��
��![]() ����
����![]() ��
��![]() ��
��
����![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����タC1��y��![]() x2(p>0)�Ľ��c(di��n)�c�p����C2��
x2(p>0)�Ľ��c(di��n)�c�p����C2��![]() ��y2��1���ҽ��c(di��n)���B����C1�ڵ�һ�����c(di��n)M.��C1���c(di��n)M̎���о�ƽ����C2��һ�l�u�������tp��( )��
��y2��1���ҽ��c(di��n)���B����C1�ڵ�һ�����c(di��n)M.��C1���c(di��n)M̎���о�ƽ����C2��һ�l�u�������tp��( )��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����߅��![]() �c
�c![]() ��������
��������![]() ����
����![]() .
.
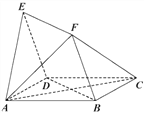
�������C��![]() ƽ��
ƽ��![]() ��
��
����������![]() ������ֵ��
������ֵ��
������![]() �龀��
�龀��![]() �ϵ�һ�c(di��n)���ҝM��ֱ��
�ϵ�һ�c(di��n)���ҝM��ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() ����
����![]() ���L(zh��ng).
���L(zh��ng).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ڼס��҃ɂ�(g��)�༉(j��)�M(j��n)�Д�(sh��)�W(xu��)��ԇ�����մ��ڵ���120�֞郞(y��u)�㣬120������ǃ�(y��u)��y(t��ng)Ӌ(j��)�ɿ�(j��)�õ����µ�2��2��(li��n)������֪��ȫ��105���г鵽�S�C(j��)��ȡ1�˞郞(y��u)��ĸ��ʞ�![]() ��
��
��(y��u)�� | �ǃ�(y��u)�� | ��Ӌ(j��) | |
�װ� | 10 | ||
�Ұ� | 30 | ||
��Ӌ(j��) |
��1��Ո(q��ng)����������(li��n)����
��2������(j��)��(li��n)���Ĕ�(sh��)��(j��)������95%�Ŀ�����Ҫ���ܷ��J(r��n)�顰�ɿ�(j��)�c�༉(j��)���P(gu��n)ϵ����
P��K2��x0�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
������ʽ����(sh��)��(j��)��K2=![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�̵�ÿ�죨�_ʼ�I(y��ng)�I(y��)�r(sh��)����ÿ��15Ԫ�ăr(ji��)��ُ(g��u)��![]() ��Ʒ���ɣ�
��Ʒ���ɣ�![]() ��Ʒ���̵�ı��r�r(sh��)�g��8С�r(sh��)��ԓ�̵�ĠI(y��ng)�I(y��)�r(sh��)�gҲǡ�Þ�8С�r(sh��)�������_ʼ��ÿ��30Ԫ�ăr(ji��)����ۣ���ǰ6С�r(sh��)��(n��i)��ُ(g��u)�M(j��n)��
��Ʒ���̵�ı��r�r(sh��)�g��8С�r(sh��)��ԓ�̵�ĠI(y��ng)�I(y��)�r(sh��)�gҲǡ�Þ�8С�r(sh��)�������_ʼ��ÿ��30Ԫ�ăr(ji��)����ۣ���ǰ6С�r(sh��)��(n��i)��ُ(g��u)�M(j��n)��![]() ��Ʒ�]�����꣬�t�̵ꌦ(du��)�]�u����
��Ʒ�]�����꣬�t�̵ꌦ(du��)�]�u����![]() ��Ʒ����ÿ��10Ԫ�ăr(ji��)��̓r(ji��)̎���ꮅ������(j��)��(j��ng)�(y��n)��2С�r(sh��)��(n��i)��ȫ�܉��
��Ʒ����ÿ��10Ԫ�ăr(ji��)��̓r(ji��)̎���ꮅ������(j��)��(j��ng)�(y��n)��2С�r(sh��)��(n��i)��ȫ�܉��![]() ��Ʒ�̓r(ji��)̎���ꮅ����̎���ꮅ��(d��ng)�첻��ُ(g��u)�M(j��n)
��Ʒ�̓r(ji��)̎���ꮅ����̎���ꮅ��(d��ng)�첻��ُ(g��u)�M(j��n)![]() ��Ʒ��.ԓ�̵�y(t��ng)Ӌ(j��)��100��
��Ʒ��.ԓ�̵�y(t��ng)Ӌ(j��)��100��![]() ��Ʒ��ÿ���ǰ6С�r(sh��)��(n��i)���N����������ij�Nԭ���N�����l��(sh��)���еIJ���?j��n)?sh��)��(j��)���ۓp�����ܿ��壬�Ƴ����±���ע��ҕ�l�ʞ���ʣ�.
��Ʒ��ÿ���ǰ6С�r(sh��)��(n��i)���N����������ij�Nԭ���N�����l��(sh��)���еIJ���?j��n)?sh��)��(j��)���ۓp�����ܿ��壬�Ƴ����±���ע��ҕ�l�ʞ���ʣ�.
ǰ6С�r(sh��)��(n��i)���N���� ����λ������ | 3 | 4 | 5 |
�l��(sh��) | 30 |
|
|
��1����ij���̵�ُ(g��u)�M(j��n)![]() ��Ʒ4����ԇ���̵�ԓ���N��
��Ʒ4����ԇ���̵�ԓ���N��![]() ��Ʒ�@ȡ����(r��n)
��Ʒ�@ȡ����(r��n)![]() �ķֲ��к�������
�ķֲ��к�������
��2�����̵�ÿ����ُ(g��u)�M(j��n)4��![]() ��Ʒ�r(sh��)���@�õ�ƽ������(r��n)�����
��Ʒ�r(sh��)���@�õ�ƽ������(r��n)�����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij܇�g���U�ס��҃ɷN�O(sh��)�����a(ch��n)A��B��a(ch��n)Ʒ���N�O(sh��)��ÿ�������a(ch��n)Aa(ch��n)Ʒ8����Ba(ch��n)Ʒ15�����ҷN�O(sh��)��ÿ�������a(ch��n)Aa(ch��n)Ʒ10����Ba(ch��n)Ʒ25������֪�O(sh��)���ÿ������U�M(f��i)300Ԫ���O(sh��)����ÿ������U�M(f��i)400Ԫ���F(xi��n)܇�g����Ҫ���a(ch��n)Aa(ch��n)Ʒ100����Ba(ch��n)Ʒ200�����������U�M(f��i)���ٞ�__Ԫ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ֱ������![]() �У�
��![]() ��
��![]() ��
��![]() �քe��
�քe��![]() �����c(di��n)��
�����c(di��n)��
��1���C����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2���������F![]() �ĸߣ�
�ĸߣ�

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����������^����ʹ��������������������������_������ ��
A. ƽ���(n��i)�����lֱ��![]() ����
����![]() ���t
���t![]() .��Ƴ������g�е����lֱ��
.��Ƴ������g�е����lֱ��![]() ����
����![]() ���t
���t![]()
B. ƽ���(n��i)�����lֱ��![]() ����
����![]() ���t
���t![]() .��Ƴ������g�е����l����
.��Ƴ������g�е����l����![]() ����
����![]() ���t
���t![]()
C. ��ƽ���(n��i)����ɂ�(g��)�������ε�߅�L(zh��ng)�ıȞ�![]() ���t��������e�Ȟ�
���t��������e�Ȟ�![]() .��Ƴ����ڿ��g�У���ɂ�(g��)�������w�����L(zh��ng)�ıȞ�
.��Ƴ����ڿ��g�У���ɂ�(g��)�������w�����L(zh��ng)�ıȞ�![]() ���t�������w�e�Ȟ�
���t�������w�e�Ȟ�![]()
D. ��![]() ���t��(f��)��(sh��)
���t��(f��)��(sh��)![]() .�����������
.�����������![]() ���t
���t![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij��У���ЌW(xu��)��15000�ˣ���������10500�ˣ�Ů��4500�ˣ����{(di��o)��ԓУ�W(xu��)��ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g����r�����÷ӳ�ӵķ������ռ�200λ�W(xu��)��ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g�Ęӱ���(sh��)��(j��)(��λ��С�r(sh��))��
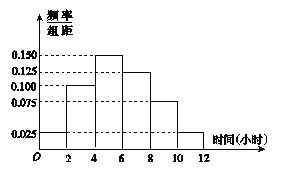
��1����(y��ng)�ռ�����λŮ���Ęӱ���(sh��)��(j��)��
��2������(j��)�@200��(g��)�ӱ���(sh��)��(j��)���õ��W(xu��)��ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g���l�ʷֲ�ֱ���D�����Иӱ���(sh��)��(j��)�ķֽM�^(q��)�g�飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����Ӌ(j��)ԓУ�W(xu��)��ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g���^4С�r(sh��)�ĸ��ʣ�
����Ӌ(j��)ԓУ�W(xu��)��ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g���^4С�r(sh��)�ĸ��ʣ�
��3���ژӱ���(sh��)��(j��)�У���40λŮ����ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g���^4С�r(sh��)��Ո(q��ng)���ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g�c�Ԅe��(li��n)�������Д��Ƿ���95���İ����J(r��n)����ԓУ�W(xu��)����ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g�c�Ԅe���P(gu��n)�������ѱ���(ji��n)Ҫ���ڴ��}���ϣ�
���� | Ů�� | ��Ӌ(j��) | |
ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g�����^4С�r(sh��) | |||
ÿ��ƽ���w���\(y��n)��(d��ng)�r(sh��)�g���^4С�r(sh��) | |||
��Ӌ(j��) |
����
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
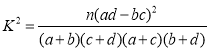
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com