【題目】《中國詩詞大會》是央視首檔全民參與的詩詞節目，節目以“賞中華詩詞，尋文化基因，品生活之美”為宗旨.每一期的比賽包含以下環節：“個人追逐賽”、“攻擂資格爭奪賽”和“擂主爭霸賽”，其中“擂主爭霸賽”由“攻擂資格爭奪賽”獲勝者與上一場擂主進行比拼.“擂主爭霸賽”共有九道搶答題，搶到并答對者得一分，答錯則對方得一分，率先獲得五分者即為該場擂主.在《中國詩詞大會》的某一期節目中，若進行“擂主爭霸賽”的甲乙兩位選手每道搶答題得到一分的概率都是為0.5，則搶答完七道題后甲成為擂主的概率為________.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中曲線
的參數方程為
（
為參數），以
為極點，
軸的正半軸為極軸，建立極坐標系，直線
的極坐標方程為
.
（1）求曲線的普通方程以及直線的直角坐標方程；
（2）將曲線向左平移2個單位，再將曲線上的所有點的橫坐標縮短為原來的
，得到曲線
，求曲線上的點到直線的距離的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題10分）選修4—4：坐標系與參數方程
已知曲線C1的參數方程為
（t為參數），以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，曲線C2的極坐標方程為ρ=2sinθ。
（Ⅰ）把C1的參數方程化為極坐標方程；
（Ⅱ）求C1與C2交點的極坐標（ρ≥0,0≤θ＜2π）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)=|x﹣1|+|2x﹣6|(x∈R)，記f(x)的最小值為c.
（1）求c的值;
（2）若實數ab滿足a>0,b>0，a+b=c，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，一個湖的邊界是圓心為
的圓，湖的一側有一條直線型公路
，湖上有橋
（是圓的直徑）．規劃在公路上選兩個點
，
，并修建兩段直線型道路
，
，規劃要求：線段，上的所有點到點的距離均不小于圓的半徑．已知點
，
到直線的距離分別為
和
（
，
為垂足），測得
，
，
（單位：百米）．
（1）若道路與橋垂直，求道路的長；
（2）在規劃要求下，和中能否有一個點選在處？并說明理由；
（3）在規劃要求下，若道路和的長度均為
（單位：百米），求當最小時，、兩點間的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動點
滿足： 
.
（1）求動點
的軌跡
的方程；
（2）設過點
的直線
與曲線
交于
兩點，點
關于
軸的對稱點為
（點
與點
不重合），證明：直線
恒過定點，并求該定點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設各項均為正數的數列{an}的前n項和為Sn，已知a1＝1，且anSn+1﹣an+1Sn＝an+1﹣λan，對一切n∈N*都成立.
（1）當λ＝1時；
①求數列{an}的通項公式；
②若bn＝（n+1）an，求數列{bn}的前n項的和Tn；
（2）是否存在實數λ，使數列{an}是等差數列如果存在，求出λ的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某網店經營各種兒童玩具，該網店老板發現該店經銷的一種手腕可以搖動的
款芭比娃娃玩具在某周內所獲純利
（元）與該周每天銷售這種芭比娃娃的個數
（個）之間的關系如下表：
每天銷售芭比娃娃個數 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
該周內所獲純利 | 66 | 69 | 74 | 81 | 89 | 90 | 91 |
（1）由表中數據可推測
線性相關，求出回歸直線方程；
（2）請你預測當該店每天銷售這種芭比娃娃20件時，每周獲純利多少？
參考公式：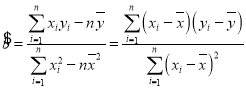
，
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
