
【題目】已知![]() 是橢圓
是橢圓![]() 上的兩點.
上的兩點.
(1)求橢圓![]() 的離心率;
的離心率;
(2)已知直線![]() 過點
過點![]() ,且與橢圓
,且與橢圓![]() 交于另一點
交于另一點![]() (不同于點
(不同于點![]() ),若以
),若以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)將A和B點的坐標代入橢圓G的方程,列出方程組求出![]() 的值,再求出
的值,再求出![]() 和離心率;
和離心率;
(2)由(1)求出橢圓G的方程,對直線![]() 的斜率進行討論,不妨設直線
的斜率進行討論,不妨設直線![]() 的方程,與橢圓G的方程聯立后,利用韋達定理寫出式子,將條件轉化為
的方程,與橢圓G的方程聯立后,利用韋達定理寫出式子,將條件轉化為![]() ,由向量數量積的坐標運算列出式子,代入化簡后求出
,由向量數量積的坐標運算列出式子,代入化簡后求出![]() 的值,即得直線
的值,即得直線![]() 的方程.
的方程.
解:(1)由已知![]() ,
,
由點![]() 在橢圓
在橢圓![]() 上可得
上可得![]() ,
,
解得![]() .
.
所以![]() ,
,
所以橢圓![]() 的離心率是
的離心率是![]() ;
;
(2)當直線![]() 過點
過點![]() 且斜率不存在時,可得點
且斜率不存在時,可得點![]() ,不滿足條件;
,不滿足條件;
設直線![]() 的方程為
的方程為![]() ),點
),點![]() ,
,
由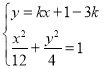 可得
可得![]() ,
,
顯然![]() ,此方程兩個根是點
,此方程兩個根是點![]() 和點
和點![]() 的橫坐標,
的橫坐標,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
因為以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,
,
所以![]() ,即
,即![]() ,
,
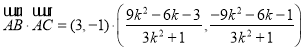
![]() ,
,
即![]() ,
,
![]() ,
,![]() ,
,
當![]() 時,即直線
時,即直線![]() ,與已知點
,與已知點![]() 不同于點
不同于點![]() 矛盾,
矛盾,
所以![]() ,
,
所以直線![]() 的方程為
的方程為![]() .
.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:高中數學 來源: 題型:
【題目】2018年,某地認真貫徹落實中央十九大精神和各項宏觀調控政策,經濟運行平穩增長,民生保障持續加強,惠民富民成效顯著,城鎮居民收入穩步增長,收入結構穩中趨優.據當地統計局公布的數據,現將8月份至12月份當地的人均月收入增長率與人均月收入分別繪制成折線圖(如圖一)與不完整的條形統計圖(如圖二).請從圖中提取相關的信息:
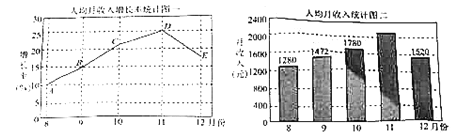
①10月份人均月收入增長率為![]() 左右;
左右;
②11月份人均月收入為2047元;
③從上圖可知該地9月份至12月份人均月收入比8月份人均月收入均得到提高.
其中正確的信息個數為( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1:y=cos x,C2:y=sin (2x+![]() ),則下面結論正確的是( )
),則下面結論正確的是( )
A. 把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
B. 把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
C. 把C1上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向右平移
倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
D. 把C1上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向左平移
倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是公比為 q的等比數列,且a1,a3,a2成等差數列.
(Ⅰ)求q的值;
(Ⅱ)設{bn}是以2為首項,q為公差的等差數列,其前n項和為Sn,當n≥2時,比較Sn與bn的大小,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(﹣1,0),B(1,0),C(0,1),直線y=ax+b(a>0)將△ABC分割為面積相等的兩部分,則b的取值范圍是( )
A.(0,1)B. C.
C. D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 上一點
上一點![]() 到焦點
到焦點![]() 的距離
的距離![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)過點![]() 引圓
引圓![]() 的兩條切線
的兩條切線![]() ,切線
,切線![]() 與拋物線
與拋物線![]() 的另一交點分別為
的另一交點分別為![]() ,線段
,線段![]() 中點的橫坐標記為
中點的橫坐標記為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司對一個擁有20000人的企業推出一款意外險產品,每年每位職工只要交少量保費,發生意外后可一次性獲得若干賠償金,保險公司把企業的所有崗位共分為![]() 三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
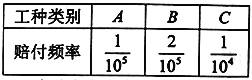
已知![]() 三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
(1)求保險公司在該業務所或利潤的期望值;
(2)現有如下兩個方案供企業選擇:
方案1:企業不與保險公司合作,職工不交保險,出意外企業自行拿出與保險公司提供的等額賠償金賠償付給意外職工,企業開展這項工作的固定支出為每年12萬元;
方案2:企業與保險公司合作,企業負責職工保費的70%,職工個人負責保費的30%,出險后賠償金由保險公司賠付,企業無額外專項開支.
請根據企業成本差異給出選擇合適方案的建議.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com