
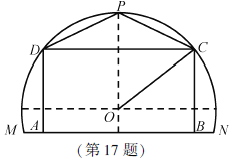
【題目】某農(nóng)場(chǎng)有一塊農(nóng)田,如圖所示,它的邊界由圓O的一段圓弧![]() (P為此圓弧的中點(diǎn))和線段MN構(gòu)成.已知圓O的半徑為40米,點(diǎn)P到MN的距離為50米.現(xiàn)規(guī)劃在此農(nóng)田上修建兩個(gè)溫室大棚,大棚Ⅰ內(nèi)的地塊形狀為矩形ABCD,大棚Ⅱ內(nèi)的地塊形狀為
(P為此圓弧的中點(diǎn))和線段MN構(gòu)成.已知圓O的半徑為40米,點(diǎn)P到MN的距離為50米.現(xiàn)規(guī)劃在此農(nóng)田上修建兩個(gè)溫室大棚,大棚Ⅰ內(nèi)的地塊形狀為矩形ABCD,大棚Ⅱ內(nèi)的地塊形狀為![]() ,要求
,要求![]() 均在線段
均在線段![]() 上,
上,![]() 均在圓弧上.設(shè)OC與MN所成的角為
均在圓弧上.設(shè)OC與MN所成的角為![]() .
.
(1)用![]() 分別表示矩形
分別表示矩形![]() 和
和![]() 的面積,并確定
的面積,并確定![]() 的取值范圍;
的取值范圍;
(2)若大棚Ⅰ內(nèi)種植甲種蔬菜,大棚Ⅱ內(nèi)種植乙種蔬菜,且甲、乙兩種蔬菜的單位面積年產(chǎn)值之比為![]() .求當(dāng)
.求當(dāng)![]() 為何值時(shí),能使甲、乙兩種蔬菜的年總產(chǎn)值最大.
為何值時(shí),能使甲、乙兩種蔬菜的年總產(chǎn)值最大.
【答案】(1)矩形ABCD的面積為800(4sinθcosθ+cosθ)平方米,△CDP的面積為
1600(cosθ–sinθcosθ),sinθ的取值范圍是[![]() ,1).
,1).
(2)當(dāng)θ=![]() 時(shí),能使甲、乙兩種蔬菜的年總產(chǎn)值最大
時(shí),能使甲、乙兩種蔬菜的年總產(chǎn)值最大
【解析】分析:(1)先根據(jù)條件求矩形長與寬,三角形的底與高,再根據(jù)矩形面積公式以及三角形面積公式得結(jié)果,最后根據(jù)實(shí)際意義確定![]() 的取值范圍;(2)根據(jù)條件列函數(shù)關(guān)系式,利用導(dǎo)數(shù)求極值點(diǎn),再根據(jù)單調(diào)性確定函數(shù)最值取法.
的取值范圍;(2)根據(jù)條件列函數(shù)關(guān)系式,利用導(dǎo)數(shù)求極值點(diǎn),再根據(jù)單調(diào)性確定函數(shù)最值取法.
詳解: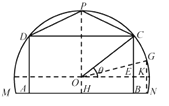
解:(1)連結(jié)PO并延長交MN于H,則PH⊥MN,所以OH=10.
過O作OE⊥BC于E,則OE∥MN,所以∠COE=θ,
故OE=40cosθ,EC=40sinθ,
則矩形ABCD的面積為2×40cosθ(40sinθ+10)=800(4sinθcosθ+cosθ),
△CDP的面積為![]() ×2×40cosθ(40–40sinθ)=1600(cosθ–sinθcosθ).
×2×40cosθ(40–40sinθ)=1600(cosθ–sinθcosθ).
過N作GN⊥MN,分別交圓弧和OE的延長線于G和K,則GK=KN=10.
令∠GOK=θ0,則sinθ0=![]() ,θ0∈(0,
,θ0∈(0,![]() ).
).
當(dāng)θ∈[θ0,![]() )時(shí),才能作出滿足條件的矩形ABCD,
)時(shí),才能作出滿足條件的矩形ABCD,
所以sinθ的取值范圍是[![]() ,1).
,1).
答:矩形ABCD的面積為800(4sinθcosθ+cosθ)平方米,△CDP的面積為
1600(cosθ–sinθcosθ),sinθ的取值范圍是[![]() ,1).
,1).
(2)因?yàn)榧住⒁覂煞N蔬菜的單位面積年產(chǎn)值之比為4∶3,
設(shè)甲的單位面積的年產(chǎn)值為4k,乙的單位面積的年產(chǎn)值為3k(k>0),
則年總產(chǎn)值為4k×800(4sinθcosθ+cosθ)+3k×1600(cosθ–sinθcosθ)
=8000k(sinθcosθ+cosθ),θ∈[θ0,![]() ).
).
設(shè)f(θ)= sinθcosθ+cosθ,θ∈[θ0,![]() ),
),
則![]() .
.
令![]() ,得θ=
,得θ=![]() ,
,
當(dāng)θ∈(θ0,![]() )時(shí),
)時(shí),![]() ,所以f(θ)為增函數(shù);
,所以f(θ)為增函數(shù);
當(dāng)θ∈(![]() ,
,![]() )時(shí),
)時(shí),![]() ,所以f(θ)為減函數(shù),
,所以f(θ)為減函數(shù),
因此,當(dāng)θ=![]() 時(shí),f(θ)取到最大值.
時(shí),f(θ)取到最大值.
答:當(dāng)θ=![]() 時(shí),能使甲、乙兩種蔬菜的年總產(chǎn)值最大.
時(shí),能使甲、乙兩種蔬菜的年總產(chǎn)值最大.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() 上有一動(dòng)點(diǎn)
上有一動(dòng)點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作直線
作直線![]() 垂直于
垂直于![]() 軸,動(dòng)點(diǎn)
軸,動(dòng)點(diǎn)![]() 在
在![]() 上,且滿足
上,且滿足![]() (
(![]() 為坐標(biāo)原點(diǎn)),記點(diǎn)
為坐標(biāo)原點(diǎn)),記點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)已知定點(diǎn)![]() ,
,![]() ,
,![]() 為曲線
為曲線![]() 上一點(diǎn),直線
上一點(diǎn),直線![]() 交曲線
交曲線![]() 于另一點(diǎn)
于另一點(diǎn)![]() ,且點(diǎn)
,且點(diǎn)![]() 在線段
在線段![]() 上,直線
上,直線![]() 交曲線
交曲線![]() 于另一點(diǎn)
于另一點(diǎn)![]() ,求
,求![]() 的內(nèi)切圓半徑
的內(nèi)切圓半徑![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】古希臘著名數(shù)學(xué)家阿波羅尼斯與歐幾里得、阿基米德齊名.他發(fā)現(xiàn):“平面內(nèi)到兩個(gè)定點(diǎn)![]() 的距離之比為定值
的距離之比為定值![]() 的點(diǎn)的軌跡是圓”.后來,人們將這個(gè)圓以他的名字命名,稱為阿波羅尼斯圓,簡(jiǎn)稱阿氏圓在平面直角坐標(biāo)系
的點(diǎn)的軌跡是圓”.后來,人們將這個(gè)圓以他的名字命名,稱為阿波羅尼斯圓,簡(jiǎn)稱阿氏圓在平面直角坐標(biāo)系![]() 中,
中,![]() 點(diǎn)
點(diǎn)![]() .設(shè)點(diǎn)
.設(shè)點(diǎn)![]() 的軌跡為
的軌跡為![]() ,下列結(jié)論正確的是( )
,下列結(jié)論正確的是( )
A. ![]() 的方程為
的方程為![]()
B. 在![]() 軸上存在異于
軸上存在異于![]() 的兩定點(diǎn)
的兩定點(diǎn)![]() ,使得
,使得![]()
C. 當(dāng)![]() 三點(diǎn)不共線時(shí),射線
三點(diǎn)不共線時(shí),射線![]() 是
是![]() 的平分線
的平分線
D. 在![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,角
中,角![]() ,
,![]() ,
,![]() 所對(duì)的邊分別為
所對(duì)的邊分別為![]() ,
,![]() ,
,![]() ,且
,且![]() ,則下列結(jié)論正確的是( )
,則下列結(jié)論正確的是( )
A.![]() B.
B.![]() 是鈍角三角形
是鈍角三角形
C.![]() 的最大內(nèi)角是最小內(nèi)角的
的最大內(nèi)角是最小內(nèi)角的![]() 倍D.若
倍D.若![]() ,則
,則![]() 外接圓半徑為
外接圓半徑為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著互聯(lián)網(wǎng)金融的不斷發(fā)展,很多互聯(lián)網(wǎng)公司推出余額增值服務(wù)產(chǎn)品和活期資金管理服務(wù)產(chǎn)品,如螞蟻金服旗下的“余額寶”,騰訊旗下的“財(cái)富通”,京東旗下“京東小金庫”.為了調(diào)查廣大市民理財(cái)產(chǎn)品的選擇情況,隨機(jī)抽取1200名使用理財(cái)產(chǎn)品的市民,按照使用理財(cái)產(chǎn)品的情況統(tǒng)計(jì)得到如下頻數(shù)分布表:
分組 | 頻數(shù)(單位:名) |
使用“余額寶” |
|
使用“財(cái)富通” |
|
使用“京東小金庫” | 30 |
使用其他理財(cái)產(chǎn)品 | 50 |
合計(jì) | 1200 |
已知這1200名市民中,使用“余額寶”的人比使用“財(cái)富通”的人多160名.
(1)求頻數(shù)分布表中![]() ,
,![]() 的值;
的值;
(2)已知2018年“余額寶”的平均年化收益率為![]() ,“財(cái)富通”的平均年化收益率為
,“財(cái)富通”的平均年化收益率為![]() .若在1200名使用理財(cái)產(chǎn)品的市民中,從使用“余額寶”和使用“財(cái)富通”的市民中按分組用分層抽樣方法共抽取7人,然后從這7人中隨機(jī)選取2人,假設(shè)這2人中每個(gè)人理財(cái)?shù)馁Y金有10000元,這2名市民2018年理財(cái)?shù)睦⒖偤蜑?/span>
.若在1200名使用理財(cái)產(chǎn)品的市民中,從使用“余額寶”和使用“財(cái)富通”的市民中按分組用分層抽樣方法共抽取7人,然后從這7人中隨機(jī)選取2人,假設(shè)這2人中每個(gè)人理財(cái)?shù)馁Y金有10000元,這2名市民2018年理財(cái)?shù)睦⒖偤蜑?/span>![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望.注:平均年化收益率,也就是我們所熟知的利息,理財(cái)產(chǎn)品“平均年化收益率為
的分布列及數(shù)學(xué)期望.注:平均年化收益率,也就是我們所熟知的利息,理財(cái)產(chǎn)品“平均年化收益率為![]() ”即將100元錢存入某理財(cái)產(chǎn)品,一年可以獲得3元利息.
”即將100元錢存入某理財(cái)產(chǎn)品,一年可以獲得3元利息.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)若當(dāng)![]() 時(shí),
時(shí),![]() 取得極值,求
取得極值,求![]() 的值,并求
的值,并求![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
(2)若![]() 存在兩個(gè)極值點(diǎn)
存在兩個(gè)極值點(diǎn)![]() ,求
,求![]() 的取值范圍,并證明:
的取值范圍,并證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商場(chǎng)為改進(jìn)服務(wù)質(zhì)量,在進(jìn)場(chǎng)購物的顧客中隨機(jī)抽取了![]() 人進(jìn)行問卷調(diào)查.調(diào)查后,就顧客“購物體驗(yàn)”的滿意度統(tǒng)計(jì)如下:
人進(jìn)行問卷調(diào)查.調(diào)查后,就顧客“購物體驗(yàn)”的滿意度統(tǒng)計(jì)如下:
滿意 | 不滿意 | |
男 |
|
|
女 |
|
|
![]() 是否有
是否有![]() 的把握認(rèn)為顧客購物體驗(yàn)的滿意度與性別有關(guān)?
的把握認(rèn)為顧客購物體驗(yàn)的滿意度與性別有關(guān)?
![]() 若在購物體驗(yàn)滿意的問卷顧客中按照性別分層抽取了
若在購物體驗(yàn)滿意的問卷顧客中按照性別分層抽取了![]() 人發(fā)放價(jià)值
人發(fā)放價(jià)值![]() 元的購物券.若在獲得了
元的購物券.若在獲得了![]() 元購物券的
元購物券的![]() 人中隨機(jī)抽取
人中隨機(jī)抽取![]() 人贈(zèng)其紀(jì)念品,求獲得紀(jì)念品的
人贈(zèng)其紀(jì)念品,求獲得紀(jì)念品的![]() 人中僅有
人中僅有![]() 人是女顧客的概率.
人是女顧客的概率.
附表及公式: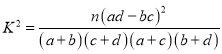 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() 為自然對(duì)數(shù)的底數(shù),則函數(shù)
為自然對(duì)數(shù)的底數(shù),則函數(shù)
![]()
![]() 的零點(diǎn)個(gè)數(shù)為( )
的零點(diǎn)個(gè)數(shù)為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,橢圓![]()
![]() 的左焦點(diǎn)為
的左焦點(diǎn)為![]() ,右頂點(diǎn)為
,右頂點(diǎn)為![]() ,上頂點(diǎn)為
,上頂點(diǎn)為![]() .
.
(1)已知橢圓的離心率為![]() ,線段
,線段![]() 中點(diǎn)的橫坐標(biāo)為
中點(diǎn)的橫坐標(biāo)為![]() ,求橢圓的標(biāo)準(zhǔn)方程;
,求橢圓的標(biāo)準(zhǔn)方程;
(2)已知△![]() 外接圓的圓心在直線
外接圓的圓心在直線![]() 上,求橢圓的離心率
上,求橢圓的離心率![]() 的值.
的值.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com