
����С�}�M��14�֣�
��ƽ��ֱ������(bi��o)ϵ �У��E�A
�У��E�A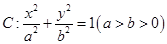 ���x���ʞ�
���x���ʞ� ��ֱ��
��ֱ��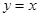 ���E�A
���E�A �صõľ����L(zh��ng)��
�صõľ����L(zh��ng)��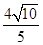 .
.
������E�A �ķ��̣�
�ķ��̣�
�����^ԭ�c(di��n)��ֱ���c�E�A ����
����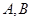 ���c(di��n)��
���c(di��n)��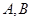 ���ǙE�A
���ǙE�A ����c(di��n)��.�c(di��n)
����c(di��n)��.�c(di��n)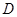 �ڙE�A
�ڙE�A �ϣ���
�ϣ���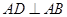 ��ֱ��
��ֱ��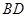 �c
�c �S��
�S�� �S�քe����
�S�քe����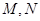 ���c(di��n).
���c(di��n).
��i���O(sh��)ֱ��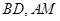 ��б�ʷքe��
��б�ʷքe��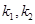 ���C�����ڳ���(sh��)
���C�����ڳ���(sh��)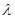 ʹ��
ʹ��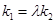 �������
�������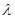 ��ֵ��
��ֵ��
��ii����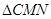 ��e�����ֵ.
��e�����ֵ.
��1��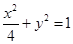 .��2�����������ڳ���(sh��)
.��2�����������ڳ���(sh��)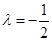 ʹ�ýY(ji��)Փ����.������
ʹ�ýY(ji��)Փ����.������ .
.
����ԇ�}��������1���������}��õ� ����
����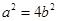 .
.
��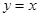 ����
���� �ɵ�
�ɵ�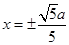 ��
��
�� ���ɵ�
���ɵ� .
.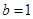 �ý�.
�ý�.
��2��������ע��Ĵ_��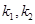 �ı��_(d��)ʽ���֣�̽��ʹ
�ı��_(d��)ʽ���֣�̽��ʹ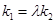 ������
������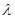 .
.
�O(sh��)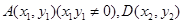 ���t
���t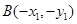 ��
��
�õ� ��
��
����(j��)ֱ��BD�ķ��̞�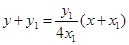 ��
��
��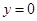 ����
����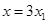 ����
����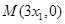 .�õ�
.�õ�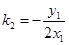 .
.
�� �������Y(ji��)Փ.
�������Y(ji��)Փ.
������ֱ��BD�ķ���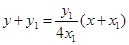 ��
��
�Ĵ_��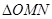 ����e���_(d��)ʽ
����e���_(d��)ʽ ���֣���(y��ng)�û�������ʽ�ý�.
���֣���(y��ng)�û�������ʽ�ý�.
ԇ�}��������1�����}��֪ ���ɵ�
���ɵ�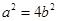 .
.
�E�AC�ķ��̿ɻ���(ji��n)�� .
.
��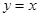 ����ɵ�
����ɵ�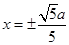 ��
��
��� ���ɵ�
���ɵ� .
.
���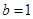 ��
��
���ԙE�AC�ķ��̞�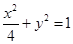 .
.
��2���������O(sh��)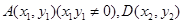 ���t
���t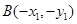 ��
��
��?y��n)�ֱ��AB��б�� ��
��
�� ������ֱ��AD��б��
������ֱ��AD��б�� ��
��
�O(sh��)ֱ��AD�ķ��̞� ��
��
���}��֪ ��
��
�� ���ɵ�
���ɵ� .
.
����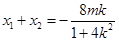 ��
��
��� ��
��
���}��֪��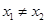
���� ��
��
����ֱ��BD�ķ��̞�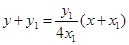 ��
��
��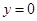 ����
����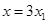 ����
����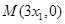 .
.
�ɵ�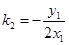 .
.
���� ����
����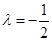 .
.
��˴��ڳ���(sh��)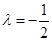 ʹ�ýY(ji��)Փ����.
ʹ�ýY(ji��)Փ����.
������ֱ��BD�ķ���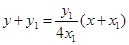 ��
��
�� ����
���� ����
���� ��
��
�ɣ�����֪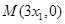 ��
��
�ɵ�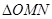 ����e
����e ��
��
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/e1/e/1xdn44.png" style="vertical-align:middle;" />����(d��ng)�҃H��(d��ng)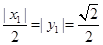 �r(sh��)��̖(h��o)������
�r(sh��)��̖(h��o)������
�˕r(sh��)Sȡ�����ֵ ��
��
����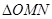 ����e�����ֵ��
����e�����ֵ�� .
.
���c(di��n)���E�A�Ď����|(zh��)��ֱ���c�E�A��λ���P(gu��n)ϵ����������e����������ʽ�đ�(y��ng)��.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
ֱ��y��kx��b�c����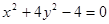 ����A��B���c(di��n)��ӛ��AOB����e��S��O������(bi��o)ԭ�c(di��n)����
����A��B���c(di��n)��ӛ��AOB����e��S��O������(bi��o)ԭ�c(di��n)����
��1�����������x���ʣ�
��2������k��0��0��b��1�ėl���£�S�����ֵ��
��3����(d��ng)��AB����2��S��1�r(sh��)����ֱ��AB�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪���タ �����}p: ֱ��l1:
�����}p: ֱ��l1: �c���タC�й����c(di��n)�����}q: ֱ��l2:
�c���タC�й����c(di��n)�����}q: ֱ��l2: �����タC���صõľ����L(zh��ng)����2����
�����タC���صõľ����L(zh��ng)����2����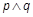 ���,
���,  ����,��k��ȡֵ������
����,��k��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�oՓ ���κΌ�(sh��)��(sh��)��ֱ��
���κΌ�(sh��)��(sh��)��ֱ��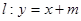 �c�p����
�c�p����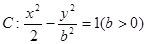 ������c(di��n).
������c(di��n).
��1�����p����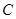 ���x����
���x���� ��ȡֵ������
��ȡֵ������
��2����ֱ�� �^�p����
�^�p����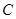 ���ҽ��c(di��n)
���ҽ��c(di��n)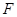 ���c�p��������
���c�p��������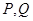 ���c(di��n)�����ҝM��
���c(di��n)�����ҝM��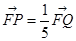 �����p����
�����p����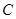 �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
���M��14�֣���D��ƽ��ֱ������(bi��o)ϵ �У�
�У� �քe�ǙE�A
�քe�ǙE�A �����ҽ��c(di��n)����c(di��n)
�����ҽ��c(di��n)����c(di��n)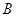 ������(bi��o)��
������(bi��o)�� ���B��
���B��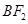 �����L(zh��ng)���E�A���c(di��n)
�����L(zh��ng)���E�A���c(di��n)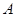 ���^�c(di��n)
���^�c(di��n)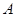 ��
�� �S�Ĵ������E�A����һ�c(di��n)
�S�Ĵ������E�A����һ�c(di��n)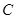 ���B��
���B�� .
.
��1�����c(di��n)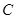 ������(bi��o)��
������(bi��o)�� ����
���� ����E�A�ķ��̣�
����E�A�ķ��̣�
��2����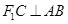 ����E�A�x����
����E�A�x���� ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)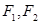 �քe�ǙE�A
�քe�ǙE�A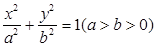 �����ҽ��c(di��n)��
�����ҽ��c(di��n)��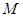 ��
��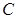 ��һ�c(di��n)��
��һ�c(di��n)��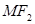 �c
�c �S��ֱ��ֱ��
�S��ֱ��ֱ��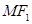 �c
�c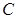 ����һ��(g��)���c(di��n)��
����һ��(g��)���c(di��n)��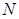 ��
��
��1����ֱ��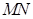 ��б�ʞ�
��б�ʞ� ����
����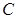 ���x���ʣ�
���x���ʣ�
��2����ֱ��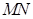 ��
��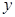 �S�ϵĽؾ���
�S�ϵĽؾ���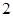 ����
����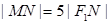 ����
����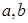 ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
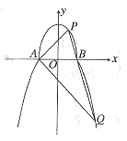
��D������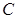 ���ϰ�E�A
���ϰ�E�A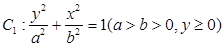 �Ͳ��֒��タ
�Ͳ��֒��タ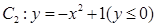 �B�Ӷ��ɣ�
�B�Ӷ��ɣ�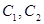 �Ĺ����c(di��n)��
�����c(di��n)��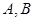 ������
������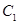 ���x���ʞ�
���x���ʞ�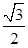 .
.
��1����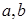 ��ֵ��
��ֵ��
��2���^�c(di��n)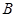 ��ֱ��
��ֱ��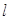 �c
�c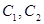 �քe����
�քe����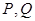 ���������c(di��n)
���������c(di��n)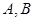 ������
������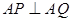 ����ֱ��
����ֱ��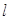 �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪P�LjA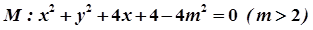 ������һ�c(di��n)���c(di��n)N������(bi��o)�飨2��0��������NP�Ĵ�ֱƽ�־���ֱ��MP���c(di��n)Q����(d��ng)�c(di��n)P�ڈAM���\(y��n)��(d��ng)�r(sh��)���c(di��n)Q��܉�E��C.
������һ�c(di��n)���c(di��n)N������(bi��o)�飨2��0��������NP�Ĵ�ֱƽ�־���ֱ��MP���c(di��n)Q����(d��ng)�c(di��n)P�ڈAM���\(y��n)��(d��ng)�r(sh��)���c(di��n)Q��܉�E��C.
��1�����܉�EC�ķ��̣���ӑՓ����C���Π
��2����(d��ng)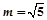 �r(sh��)����x�S���Ƿ����һ���c(di��n)E��ʹ�Ì�(du��)����C������һ�l�^E����AB��
�r(sh��)����x�S���Ƿ����һ���c(di��n)E��ʹ�Ì�(du��)����C������һ�l�^E����AB��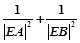 �鶨ֵ�������ڣ�������c(di��n)�Ͷ�ֵ���������ڣ�Ո(q��ng)�f������.
�鶨ֵ�������ڣ�������c(di��n)�Ͷ�ֵ���������ڣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�E�A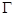 :
: ������c(di��n)��
������c(di��n)�� ,ֱ��
,ֱ��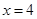 ���E�A
���E�A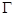 ��
��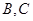 ���c(di��n)(
���c(di��n)(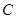 ��
��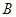 ��),��(d��ng)�c(di��n)
��),��(d��ng)�c(di��n)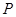 �Ͷ��c(di��n)
�Ͷ��c(di��n) ���ڙE�A
���ڙE�A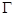 ��.
��.
(1)��E�A���̼���߅��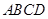 ����e.
����e.
(2)����߅��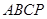 ������,���c(di��n)
������,���c(di��n)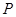 ������(bi��o).
������(bi��o).
(3)�� �錍(sh��)��(sh��),
�錍(sh��)��(sh��),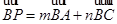 ,��
,�� ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com