
【題目】已知![]() 分別為
分別為![]() 內(nèi)角
內(nèi)角![]() 的對邊,若
的對邊,若![]() 是銳角三角形,需要同時滿足下列四個條件中的三個:
是銳角三角形,需要同時滿足下列四個條件中的三個:
①![]() ②
②![]() ③
③![]() ④
④![]()
(1)條件①④能否同時滿足,請說明理由;
(2)以上四個條件,請在滿足三角形有解的所有組合中任選一組,并求出對應的![]() 的面積.
的面積.
【答案】(1)不能,理由見解析;(2)同時滿足①②③,![]() .
.
【解析】
(1)如果條件①④能同時滿足,可知在銳角![]() 中
中![]() ,可得
,可得![]() ,即可判斷結(jié)結(jié)果;
,即可判斷結(jié)結(jié)果;
(2)由(1)知不能同時滿足①④,故只能同時滿足①②③或②③④ ;若同時滿足②③④,因為![]() ,則
,則![]() ,可得
,可得![]() ,可知不滿足題意;只能同時滿足①②③,可根據(jù)余弦定理可求出
,可知不滿足題意;只能同時滿足①②③,可根據(jù)余弦定理可求出![]() 的值,再根據(jù)三角形面積公式即可求出結(jié)果.
的值,再根據(jù)三角形面積公式即可求出結(jié)果.
解:(1)![]() 不能同時滿足①,④. 理由如下:
不能同時滿足①,④. 理由如下:
若![]() 同時滿足①,④,
同時滿足①,④,
則在銳角![]() 中,
中,![]() ,所以
,所以![]()
又因為![]() ,所以
,所以![]()
所以![]() ,這與
,這與![]() 是銳角三角形矛盾
是銳角三角形矛盾
所以![]() 不能同時滿足①,④.
不能同時滿足①,④.
(2)因為![]() 需同時滿足三個條件,由(1)知不能同時滿足①④,故只能同時滿足①②③或②③④
需同時滿足三個條件,由(1)知不能同時滿足①④,故只能同時滿足①②③或②③④
若同時滿足②③④,因為![]() ,所以
,所以![]() ,則
,則![]() ,
,
則![]() 這與
這與![]() 是銳角三角形矛盾.
是銳角三角形矛盾.
故![]() 不能同時滿足②③④,只能同時滿足①②③.
不能同時滿足②③④,只能同時滿足①②③.
因為![]() ,
,
所以![]() ,
,
解得![]() 或
或![]() .
.
當![]() 時,
時,![]() ,
,
所以![]() 為鈍角,與題意不符合,所以
為鈍角,與題意不符合,所以![]() .
.
所以![]() 的面積
的面積![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】2020年新型冠狀病毒肺炎(簡稱“新冠肺炎”)成為威脅全球的公共衛(wèi)生問題,中醫(yī)藥在本次新冠肺炎的治療中發(fā)揮了重要作用.研究人員對66例普通型新冠肺炎恢復期患者進行了中醫(yī)臨床特征分析,發(fā)現(xiàn)主要證型有氣陰兩虛證與肺脾氣虛證,同時可能兼夾濕證.為研究這兩種主要證型在兼夾濕證的難易上是否有差異,研究人員將濕證癥狀分級量化,將所有肺脾氣虛證患者的量化分作成莖葉圖.
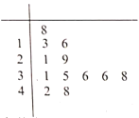
(1)若量化分不低于16分,即可診斷為兼夾濕證,請參考莖葉圖,完成下面![]() 列聯(lián)表.
列聯(lián)表.
夾濕證 | 非夾濕證 | 合計 | |
氣陰兩虛 | 20 | ||
肺脾氣虛 | |||
合計 | 66 |
(2)根據(jù)此資料,能否有99%的把握認為兩種主要證型在兼夾濕證的難易上有差異?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
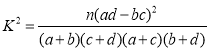
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)f(x)=ex+asinx,x∈(-π,+∞),下列說法正確的是( )
A.當a=1時,f(x)在(0,f(0))處的切線方程為2x-y+1=0
B.當a=1時,f(x)存在唯一極小值點x0且-1<f(x0)<0
C.對任意a>0,f(x)在(-π,+∞)上均存在零點
D.存在a<0,f(x)在(-π,+∞)上有且只有一個零點
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】勒洛三角形是具有類似圓的“定寬性”的曲線,它是由德國機械工程專家、機構運動學家勒洛首先發(fā)現(xiàn),其作法是:以等邊三角形每個頂點為圓心,以邊長為半徑,在另兩個頂點間作一段弧,三段弧圍成的曲邊三角形就是勒洛三角形.如圖中的兩個勒洛三角形,它們所對應的等邊三角形的邊長比為![]() ,若從大的勒洛三角形中隨機取一點,則此點取自小勒洛三角形內(nèi)的概率是( )
,若從大的勒洛三角形中隨機取一點,則此點取自小勒洛三角形內(nèi)的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.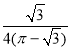
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義域均為D的三個函數(shù)![]() ,
,![]() ,
,![]() 滿足條件:對任意
滿足條件:對任意![]() ,點
,點![]() 與點
與點![]() 都關于點
都關于點![]() 對稱,則稱
對稱,則稱![]() 是
是![]() 關于
關于![]() 的“對稱函數(shù)”.已知函數(shù)
的“對稱函數(shù)”.已知函數(shù)![]() ,
,![]() ,
,![]() 是
是![]() 關于
關于![]() 的“對稱函數(shù)“,記
的“對稱函數(shù)“,記![]() 的定義域為D,若對任意
的定義域為D,若對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,則實數(shù)a的取值范圍是( )
成立,則實數(shù)a的取值范圍是( )
A..![]() B..
B..![]() C..
C..![]() D..
D..![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() ,四點
,四點![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三個點在橢圓
中恰有三個點在橢圓![]() 上,左、右焦點分別為
上,左、右焦點分別為![]() 、
、![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過左焦點![]() 且不與坐標軸平行的直線
且不與坐標軸平行的直線![]() 交橢圓于
交橢圓于![]() 、
、![]() 兩點,若線段
兩點,若線段![]() 的垂直平分線交
的垂直平分線交![]() 軸于點
軸于點![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com