設(shè)

證明

。
原命題等價于

,利用分析法。
試題分析:原命題等價于

, 10分
又

20分
故只需要證明
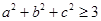
成立。 25分
利用已知條件,這是顯然的。
點評:中檔題,不等式的證明方法有,比較法、分析法、綜合法、反證法、數(shù)學(xué)歸納法、放縮法等。熟練掌握不等式的性質(zhì)是關(guān)鍵。
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知不等式
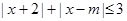
的解集為
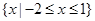
.
(Ⅰ )求
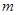
的值;
(Ⅱ )若
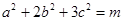
,求

的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
設(shè)

,且

,則( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
設(shè)a,b為正實數(shù),下列結(jié)論正確的是
①若a
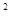
-b
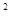
=1,則a-b<1;
②若

,則a-b<1;
③若

,則|a-b|<1;
④若|a

-b

|=1,則|a-b|<1.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
設(shè)函數(shù)
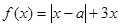
,其中
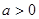
.
(1)當
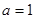
時,求不等式
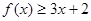
的解集;
(2)若不等式
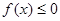
的解集為
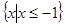
,求
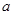
的值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若
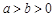
,則下列不等式一定不成立的是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知不等式
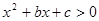
的解集為
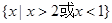
(1)求
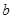
和
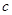
的值; (2)求不等式
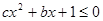
的解集.
查看答案和解析>>

 證明
證明 。
。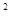 -b
-b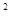 =1,則a-b<1;
=1,則a-b<1; ,則a-b<1;
,則a-b<1; ,則|a-b|<1;
,則|a-b|<1; -b
-b |=1,則|a-b|<1.
|=1,則|a-b|<1.